
已知對任意 ,
, 恒成立(其中
恒成立(其中 ),求
),求 的最大值.
的最大值.
 的最大值為
的最大值為 .
.
解析試題分析:利用二倍角公式 ,利用換元法
,利用換元法 ,將原不等式轉化為二次不等式
,將原不等式轉化為二次不等式 在區間
在區間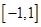 上恒成立,利用二次函數的零點分布進行討論,從而得出
上恒成立,利用二次函數的零點分布進行討論,從而得出 的最大值,但是在對
的最大值,但是在對 時的情況下,主要對二次函數的對稱軸
時的情況下,主要對二次函數的對稱軸 是否在區間
是否在區間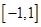 進行分類討論,再將問題轉化為
進行分類討論,再將問題轉化為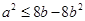 的條件下,求
的條件下,求 的最大值,
的最大值,
試題解析:由題意知 ,
,
令 ,
, ,則當
,則當 ,
, 恒成立,開口向上,
恒成立,開口向上,
①當 時,
時, ,不滿足
,不滿足 ,
, 恒成立,
恒成立,
②當 時,則必有
時,則必有 (1)
(1)
當對稱軸 時,即
時,即 ,也即
,也即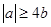 時,有
時,有 ,
,
則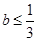 ,
, ,則
,則 ,當
,當 ,
, 時,
時, .
.
當對稱軸 時,即
時,即 ,也即
,也即 時,
時,
則必有 ,即
,即 ,又由(1)知
,又由(1)知 ,
,
則由于 ,故只需
,故只需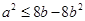 成立即可,
成立即可,
問題轉化為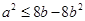 的條件下,求
的條件下,求 的最大值,然后利用代數式的結構特點或從題干中的式子出發,分別利用三角換元法、導數法以及柯西不等式法來求
的最大值,然后利用代數式的結構特點或從題干中的式子出發,分別利用三角換元法、導數法以及柯西不等式法來求 的最大值.
的最大值.
法一:(三角換元)把條件配方得: ,
, ,所以
,所以 ,
, ;
;
法二:(導數)
令 則即求函數的導數,橢圓的上半部分
則即求函數的導數,橢圓的上半部分
 ;
;
法三:(柯西不等式)由柯西不等式可知:
 ,當且僅當
,當且僅當 ,即
,即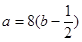 及
及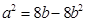 時等號成立.即當
時等號成立.即當 時,
時, 最大值為2.
最大值為2.
綜上可知 .
.
考點:1.二倍角;2.換元法;3.二次不等式的恒成立問題;4.導數;5.柯西不等式


科目:高中數學 來源: 題型:解答題
已知函數f(x)=m-|x-2|,m∈R,且f(x+2)≥0的解集為[-1,1].
(1)求m的值;
(2)若a,b,c∈R,且 =m,求證:a+2b+3c≥9.
=m,求證:a+2b+3c≥9.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com