
 (a>b>0)的第一象限上運動.
(a>b>0)的第一象限上運動. 的軌跡C1的方程;
的軌跡C1的方程; 內y=f(x)有最大值,試求橢圓C的離心率的取值范圍.
內y=f(x)有最大值,試求橢圓C的離心率的取值范圍. 的軌跡C1的方程,設
的軌跡C1的方程,設 ,只須求出x,y的關系式即可,利用點(x,y)在橢圓C:
,只須求出x,y的關系式即可,利用點(x,y)在橢圓C: (a>b>0)的第一象限上運動,點的坐標適合方程,即可得到x,y的關系式;
(a>b>0)的第一象限上運動,點的坐標適合方程,即可得到x,y的關系式; (x>0,y>0),得
(x>0,y>0),得 (x>0).利用基本不等式求出f(x)的最大值,及取得最大值的條件得出關于a,c的不等關系,即可求得橢圓C的離心率的取值范圍.
(x>0).利用基本不等式求出f(x)的最大值,及取得最大值的條件得出關于a,c的不等關系,即可求得橢圓C的離心率的取值范圍. (2分)
(2分) .
. (a>b>0)的第一象限上運動,則x>0,y>0.
(a>b>0)的第一象限上運動,則x>0,y>0. .
. (x>0,y>0).(6分)
(x>0,y>0).(6分) (x>0,y>0),得
(x>0,y>0),得 (x>0).
(x>0). ≤
≤ .
. ,即
,即 時,f(x)有最大值.(10分)
時,f(x)有最大值.(10分) 內y=f(x)有最大值,只有
內y=f(x)有最大值,只有 .(12分)
.(12分) ,解得
,解得 .
. .(14分)
.(14分)

 浙大優學小學年級銜接捷徑浙江大學出版社系列答案
浙大優學小學年級銜接捷徑浙江大學出版社系列答案科目:高中數學 來源: 題型:

查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| 2 |

| k |
| 2 |
| k |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源:2013年湖南省懷化市高考數學三模試卷(文科)(解析版) 題型:解答題
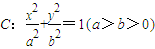 過點
過點 ,離心率
,離心率 ,若點M(x,y)在橢圓C上,則點
,若點M(x,y)在橢圓C上,則點 稱為點M的一個“橢點”,直線l交橢圓C于A、B兩點,若點A、B的“橢點”分別是P、Q,且以PQ為直徑的圓經過坐標原點O.
稱為點M的一個“橢點”,直線l交橢圓C于A、B兩點,若點A、B的“橢點”分別是P、Q,且以PQ為直徑的圓經過坐標原點O.查看答案和解析>>
科目:高中數學 來源:2013年黑龍江省哈爾濱三中高考數學二模試卷(文科)(解析版) 題型:解答題
 過點
過點 ,離心率
,離心率 ,若點M(x,y)在橢圓C上,則點
,若點M(x,y)在橢圓C上,則點 稱為點M的一個“橢點”,直線l交橢圓C于A、B兩點,若點A、B的“橢點”分別是P、Q,且以PQ為直徑的圓經過坐標原點O.
稱為點M的一個“橢點”,直線l交橢圓C于A、B兩點,若點A、B的“橢點”分別是P、Q,且以PQ為直徑的圓經過坐標原點O.查看答案和解析>>
科目:高中數學 來源:2013年黑龍江省哈爾濱三中高考數學二模試卷(理科)(解析版) 題型:解答題
 過點
過點 ,離心率
,離心率 ,若點M(x,y)在橢圓C上,則點
,若點M(x,y)在橢圓C上,則點 稱為點M的一個“橢點”,直線l交橢圓C于A、B兩點,若點A、B的“橢點”分別是P、Q,且以PQ為直徑的圓經過坐標原點O.
稱為點M的一個“橢點”,直線l交橢圓C于A、B兩點,若點A、B的“橢點”分別是P、Q,且以PQ為直徑的圓經過坐標原點O.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com