中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

(本大題共14分)一袋中裝有分別標記著1，2，3，4數字的4只小球，每次從袋中取出一只球，設每只小球被取到的可能性相同.(1)若每次取出的球不放回袋中，求恰好第三次取到標號為3的球的概率；(2)若每次取出的球放回袋中，然后再取出一只球，現連續取三次球，若三次取出的球中標號最大的數字為，求的概率分布列與期望.

(Ⅰ)    (Ⅱ)   


解析:

：(1)；……4分

(2)提示：，的分布列為：

1

2

3

4

P

(建議對1個給2分)……8分

故.……2分

練習冊系列答案
相關習題

科目：高中數學 來源：2010-2011學年年山東省棗莊市高三4模擬考試理數 題型：解答題

（本小題共14分）

已知函數

   （1）試用含有a的式子表示b，并求的單調區間；

   （2）設函數的最大值為，試證明不等式：

 （3）首先閱讀材料：對于函數圖像上的任意兩點，如果在函數圖象上存在點，使得在點M處的切線，則稱AB存在“相依切線”特別地，當時，則稱AB存在“中值相依切線”。

請問在函數的圖象上是否存在兩點，使得AB存在“中值相依切線”？若存在，求出一組A、B的坐標；若不存在，說明理由。

 

查看答案和解析>>

科目：高中數學 來源：2013屆廣東省高二下學期第一次階段考試理科數學 題型：解答題

（本小題滿分14分）某公司決定采用增加廣告投入和技術改造投入兩項措施來獲得更大的收益．通過對市場的預測，當對兩項投入都不大于3(百萬元)時，每投入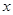(百萬元)廣告費，增加的銷售額可近似的用函數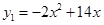(百萬元)來計算；每投入x(百萬元)技術改造費用，增加的銷售額可近似的用函數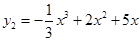(百萬元)來計算．現該公司準備共投入3(百萬元)，分別用于廣告投入和技術改造投入，請設計一種資金分配方案，使得該公司的銷售額最大． (參考數據：≈1.41，≈1.73)

 

查看答案和解析>>

科目：高中數學 來源： 題型：

（本小題共14分）

已知函數

（Ⅰ）試用含有a的式子表示b，并求的單調區間；

（Ⅱ）設函數的最大值為，試證明不等式：

（Ⅲ）首先閱讀材料：對于函數圖像上的任意兩點，如果在函數圖象上存在點，使得在點M處的切線，則稱AB存在“相依切線”特別地，當時，則稱AB存在“中值相依切線”。請問在函數的圖象上是否存在兩點，使得AB存在“中值相依切線”？若存在，求出一組A、B的坐標；若不存在，說明理由.

查看答案和解析>>

科目：高中數學 來源：2011屆年山東省棗莊市高三4模擬考試理數 題型：解答題

（本小題共14分）
已知函數
（1）試用含有a的式子表示b，并求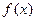的單調區間；
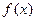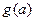（2）設函數的最大值為，試證明不等式：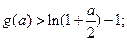
（3）首先閱讀材料：對于函數圖像上的任意兩點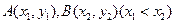，如果在函數圖象上存在點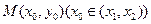，使得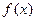在點M處的切線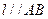，則稱AB存在“相依切線”特別地，當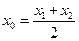時，則稱AB存在“中值相依切線”。
請問在函數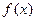的圖象上是否存在兩點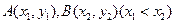，使得AB存在“中值相依切線”？若存在，求出一組A、B的坐標；若不存在，說明理由。

查看答案和解析>>

同步練習冊答案