
(本題滿分14分)已知圓 和圓外一點
和圓外一點 .
.
(1)過 作圓的割線交圓于
作圓的割線交圓于 兩點,若|
兩點,若|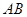 |=4,求直線
|=4,求直線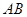 的方程;
的方程;
(2)過 作圓的切線,切點為
作圓的切線,切點為 ,求切線長及
,求切線長及 所在直線的方程.
所在直線的方程.
(1)直線 的方程
的方程 或
或 (2)切線長為
(2)切線長為
 所在直線的方程為
所在直線的方程為
【解析】
試題分析:(1)圓的方程可化為: ,圓心為
,圓心為 ,半徑
,半徑
①若割線斜率存在,設 :
: ,即
,即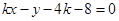 ,
,
設 的中點為
的中點為 ,則|PN|=
,則|PN|=
由 得
得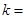
 則直線
則直線 :
: . ……4分
. ……4分
②若割線斜率不存在,則直線 :
: ,代入圓方程得
,代入圓方程得 ,
,
解得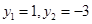 符合題意,
符合題意,
綜上,直線 的方程為
的方程為 或
或 .
……7分
.
……7分
(2)切線長為
以 為直徑的圓的方程為
為直徑的圓的方程為 ,
,
即 .
.
又已知圓的方程為 ,兩式相減,得
,兩式相減,得 ,
,
所以直線 的方程為
的方程為 .
……14分
.
……14分
考點:本小題主要考查直線與圓的位置關系、圓與圓的位置關系以及弦長公式的應用,考查學生綜合運用知識解決問題的能力和運算求解能力.
點評:要解決好此類問題就要牢固掌握直線與圓的位置關系的判斷,注重圓的幾何性質在解題的中的應用.


科目:高中數學 來源:2012-2013學年吉林省高三第一次月考文科數學試卷(解析版) 題型:解答題
(本題滿分14分)已知函數
(1)若 ,求x的值;
,求x的值;
(2)若 對于
對于 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
(本題滿分14分)
已知橢圓 :
: 的離心率為
的離心率為 ,過坐標原點
,過坐標原點 且斜率為
且斜率為 的直線
的直線 與
與 相交于
相交于 、
、 ,
, .
.
⑴求 、
、 的值;
的值;
⑵若動圓 與橢圓
與橢圓 和直線
和直線 都沒有公共點,試求
都沒有公共點,試求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
((本題滿分14分)
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
(1)當x=2時,求證:BD⊥EG ;
(2)若以F、B、C、D為頂點的三棱錐的體積記為 ,
,
求 的最大值;
的最大值;


(3)當 取得最大值時,求二面角D-BF-C的余弦值.
取得最大值時,求二面角D-BF-C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com