
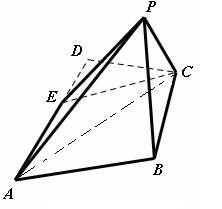
如圖, 平面
平面 ,
, ,
,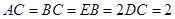 ,
, ,
, 分別為
分別為 的中點.
的中點.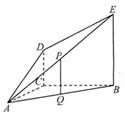
(I)證明: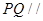 平面
平面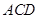 ;
;
(II)求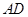 與平面
與平面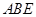 所成角的正弦值.
所成角的正弦值.
(I)只需證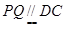 ;(II)
;(II)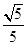 。
。
解析試題分析:(I)證明:連接 , 在
, 在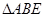 中,
中, 分別是
分別是 的中點,所以
的中點,所以 , 又
, 又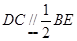 ,所以
,所以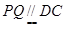 ,又
,又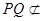 平面ACD ,DC
平面ACD ,DC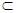 平面ACD, 所以
平面ACD, 所以 平面ACD。
平面ACD。
(Ⅱ)在 中,
中,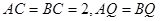 ,所以
,所以
而DC 平面ABC,
平面ABC,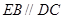 ,所以
,所以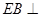 平面ABC
平面ABC
而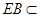 平面ABE, 所以平面ABE
平面ABE, 所以平面ABE 平面ABC, 所以
平面ABC, 所以 平面ABE
平面ABE
由(Ⅰ)知四邊形DCQP是平行四邊形,所以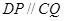
所以 平面ABE, 所以直線AD在平面ABE內的射影是AP,
平面ABE, 所以直線AD在平面ABE內的射影是AP,
所以直線AD與平面ABE所成角是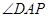
在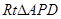 中,
中, ,
,
所以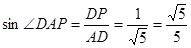 。
。
考點:線面平行的判定定理;線面角。
點評:本題主要考查了空間中直線與平面所成的角,屬立體幾何中的常考題型,較難.本題也可以用向量法來做。而對于利用向量法求線面角關鍵是正確寫出點的坐標和求解平面的一個法向量。注意計算要仔細、認真。


 舉一反三期末百分沖刺卷系列答案
舉一反三期末百分沖刺卷系列答案科目:高中數學 來源: 題型:解答題
如圖,AE⊥平面ABC,AE∥BD,AB=BC=CA=BD=2AE,F為CD中點.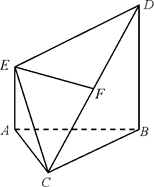
(Ⅰ)求證:EF⊥平面BCD;
(Ⅱ)求二面角C-DE-A的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在三棱柱ABC-A1B1C1中,側面ABB1A1為矩形,AB=1,AA1=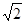 ,D為AA1中點,BD與AB1交于點O,CO丄側面ABB1A1.
,D為AA1中點,BD與AB1交于點O,CO丄側面ABB1A1.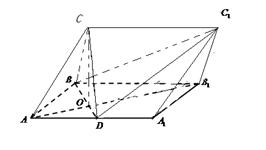
(Ⅰ)證明:BC丄AB1;
(Ⅱ)若OC=OA,求二面角C1-BD-C的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知直三棱柱ABC-A1B1C1中,AD⊥平面A1BC,其垂足D落在直線A1B上.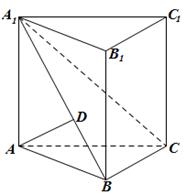
(1)求證:平面A1BC⊥平面ABB1A1;
(2)若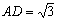 ,AB=BC=2,P為AC中點,求三棱錐
,AB=BC=2,P為AC中點,求三棱錐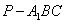 的體積。
的體積。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知菱形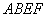 所在平面與直角梯形
所在平面與直角梯形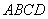 所在平面互相垂直,
所在平面互相垂直,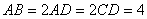 ,
,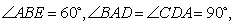 點
點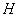 ,
,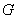 分別是線段
分別是線段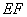 ,
, 的中點.
的中點. 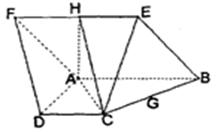
(I)求證:平面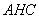
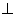 平面
平面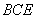 ;
;
(Ⅱ)點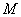 在直線
在直線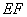 上,且
上,且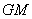 //平面
//平面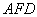 ,求平面
,求平面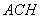 與平面
與平面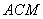 所成角的余弦值。
所成角的余弦值。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,正方形ABCD所在平面與圓O所在平面相交于CD,線段CD為圓O的弦,AE垂直于圓O所在平面,垂足E是圓O上異于C、D的點,AE=3,正方形ABCD的邊長為 .
.
(1)求證:平面ABCD丄平面ADE;
(2)求四面體BADE的體積;
(3)試判斷直線OB是否與平面CDE垂直,并請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在四邊形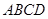 中,
中,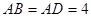 ,
,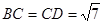 ,點
,點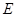 為線段
為線段 上的一點.現將
上的一點.現將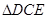 沿線段
沿線段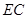 翻折到
翻折到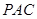 (點
(點 與點
與點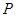 重合),使得平面
重合),使得平面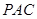
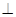 平面
平面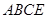 ,連接
,連接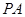 ,
,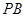 .
.
(Ⅰ)證明: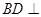 平面
平面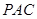 ;
;
(Ⅱ)若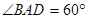 ,且點
,且點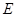 為線段
為線段 的中點,求二面角
的中點,求二面角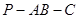 的大小.
的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com