
定義“正對數(shù)”: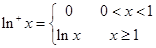 ,現(xiàn)有四個(gè)命題:
,現(xiàn)有四個(gè)命題:
①若 ,則
,則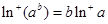
②若 ,則
,則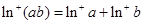
③若 ,則
,則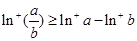
④若 ,則
,則
其中的真命題有:__________.(寫出所有真命題的編號)
①③④
解析試題分析:
因?yàn)槎x的“正對數(shù)”: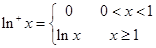 是一個(gè)分段函數(shù) ,所以對命題的判斷必須分情況討論:
是一個(gè)分段函數(shù) ,所以對命題的判斷必須分情況討論:
對于命題①(1)當(dāng) ,
,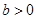 時(shí),有
時(shí),有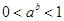 ,從而
,從而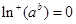 ,
,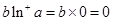 ,所以
,所以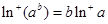 ;(2)當(dāng)
;(2)當(dāng)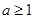 ,
,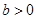 時(shí),有
時(shí),有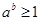 ,從而
,從而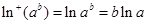 ,
,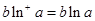 ,所以
,所以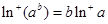 ;這樣若
;這樣若 ,則
,則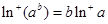 ,即命題①正確.
,即命題①正確.
對于命題②舉反例:當(dāng)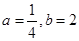 時(shí),
時(shí),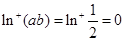 ,
,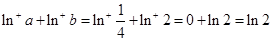
所以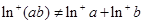 ,即命題②不正確.
,即命題②不正確.
對于命題③,首先我們通過定義可知“正對數(shù)”有以下性質(zhì):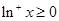 ,且
,且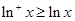 ,(1)當(dāng)
,(1)當(dāng) ,
, 時(shí),
時(shí),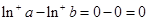 ,而
,而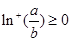 ,所以
,所以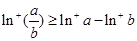 ;(2)當(dāng)
;(2)當(dāng)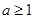 ,
, 時(shí),有
時(shí),有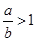 ,
,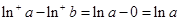 ,而
,而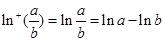 ,因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/53/09/53d09bb5cb38074562794dbe7d66ba02.png" style="vertical-align:middle;" />,所以
,因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/53/09/53d09bb5cb38074562794dbe7d66ba02.png" style="vertical-align:middle;" />,所以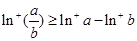 ;(3)當(dāng)
;(3)當(dāng) ,
,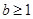 時(shí),有
時(shí),有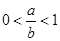 ,
,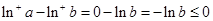 ,而
,而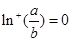 ,所以
,所以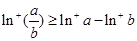 ;(4)當(dāng)
;(4)當(dāng)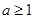 ,
,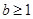 時(shí),
時(shí),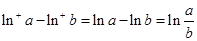 ,而
,而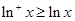 ,所以
,所以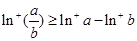 ,綜上即命題③正確.
,綜上即命題③正確.
對于命題④首先我們通過定義可知“正對數(shù)”還具有性質(zhì):若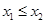 ,則
,則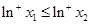 ,(1)當(dāng)
,(1)當(dāng) ,
, 時(shí),有
時(shí),有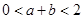 ,從而
,從而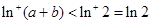 ,
,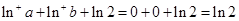 ,所以
,所以 ;(2)當(dāng)
;(2)當(dāng)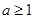 ,
, 時(shí),有
時(shí),有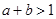 ,從而
,從而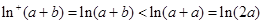 ,
,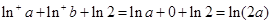



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:填空題
“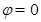 ”是“函數(shù)
”是“函數(shù)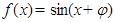 為奇函數(shù)”的 條件.
為奇函數(shù)”的 條件.
(從“充要”,“充分不必要”,“必要不充分”,“既不充分也不必要”中選擇適當(dāng)?shù)奶顚懀?/p>
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
下列四個(gè)命題中,真命題的序號有 .(寫出所有真命題的序號)
①若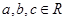 ,則“
,則“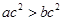 ”是“
”是“ ”成立的充分不必要條件;
”成立的充分不必要條件;
②命題“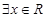 使得
使得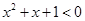 ”的否定是“
”的否定是“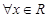 均有
均有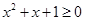 ”;
”;
③命題“若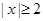 ,則
,則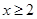 或
或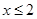 ”的否命題是“若
”的否命題是“若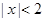 ,則
,則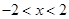 ”;
”;
④函數(shù)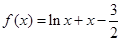 在區(qū)間
在區(qū)間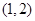 上有且僅有一個(gè)零點(diǎn).
上有且僅有一個(gè)零點(diǎn).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:填空題
已知命題p:?x∈R,使tanx=1,命題q:x2-3x+2<0的解集是{x|1<x<2}.下列結(jié)論:①命題“p∧q”是真命題; ②命題“p∧( q)”是假命題;③命題“(
q)”是假命題;③命題“( p)∨q”是真命題;④命題“(
p)∨q”是真命題;④命題“( p)∨(
p)∨( q)”是假命題.其中正確的是________.(填所有正確命題的序號)
q)”是假命題.其中正確的是________.(填所有正確命題的序號)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
已知a,b,c∈R,命題“若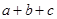 =3,則
=3,則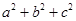 ≥3”,的否命題是 ( )
≥3”,的否命題是 ( )
A.若a+b+c≠3,則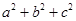 <3 <3 | B.若a+b+c=3,則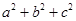 <3 <3 |
C.若a+b+c≠3,則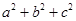 ≥3 ≥3 | D.若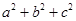 ≥3,則a+b+c=3 ≥3,則a+b+c=3 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
設(shè)函數(shù)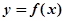 是定義域?yàn)镽的奇函數(shù),且滿足
是定義域?yàn)镽的奇函數(shù),且滿足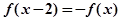 對一切
對一切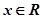 恒成立,當(dāng)
恒成立,當(dāng)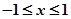 時(shí),
時(shí),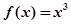 。則下列四個(gè)命題中正確的命題是
。則下列四個(gè)命題中正確的命題是
①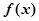 是以4為周期的周期函數(shù);②
是以4為周期的周期函數(shù);②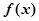 在
在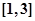 上的解析式為
上的解析式為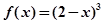 ;③
;③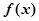 的圖象的對稱軸中有
的圖象的對稱軸中有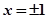 ;④
;④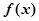 在
在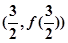 處的切線方程為
處的切線方程為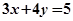 。
。
| A.①②③ | B.②③④ | C.①③④ | D.①②③④ |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:單選題
下列選項(xiàng)敘述錯(cuò)誤的是
A.命題“若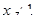 ,則 ,則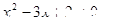 ”的逆否命題是“若 ”的逆否命題是“若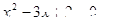 ,則 ,則 ” ” |
B.若命題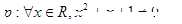 ,則 ,則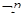 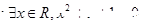 |
C.若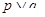 為真命題,則 為真命題,則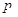 , ,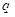 均為真命題 均為真命題 |
D.“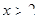 ”是“ ”是“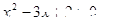 ”的充分不必要條件 ”的充分不必要條件 |
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com