
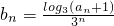 ,且Tn=b1+b2+…+bn,求Tn;
,且Tn=b1+b2+…+bn,求Tn;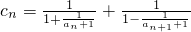 ,數(shù)列{cn}的前n項和為Mn,求證:
,數(shù)列{cn}的前n項和為Mn,求證: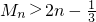 .
.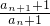 =3,
=3,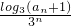 =
=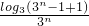 =
=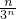 ,
, +
+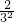 +
+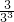 +…+
+…+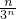 ,③
,③ Tn=
Tn= +
+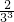 +…+
+…+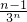 +
+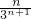 ④
④ Tn=
Tn= +
+ +…+
+…+ -
-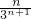 =
=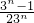 -
-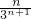 ,
, -
- •
• .
.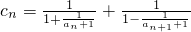
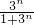 +
+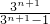
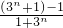 +
+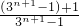
 +
+ .
.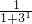 -
- )+(
)+(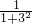 -
-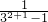 )+…+(
)+…+( -
- )].
)].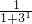 <
< ,
, >
>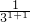 ,-
,- <-
<-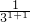 ,
,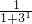 -
- <
< -
-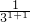 ,⑤
,⑤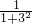 -
-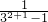 <
<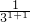 -
-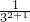 ,⑥
,⑥ -
- <
< -
-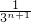 ⑦
⑦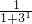 -
- )+(
)+(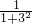 -
-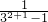 )+…+(
)+…+( -
- )<
)< -
-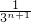 <
<
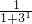 -
- )+(
)+(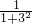 -
-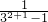 )+…+(
)+…+( -
- )]>-
)]>-
 .
.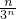 ,利用錯位相減法即可求得Tn;
,利用錯位相減法即可求得Tn; +
+ ,Mn=c1+c2+…+cn=2n-[(
,Mn=c1+c2+…+cn=2n-[(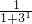 -
- )+(
)+(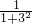 -
-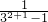 )+…+(
)+…+( -
- )].利用放縮法與累加法即可證明結(jié)論.
)].利用放縮法與累加法即可證明結(jié)論.

科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
| A、16 | B、8 | C、4 | D、不確定 |
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com