
 n∈N*, Sn,Sn+1,Sn+2不構成等比數列.
n∈N*, Sn,Sn+1,Sn+2不構成等比數列.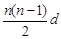 ,
,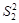 =S1
=S1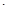 S4,即得d (2a-d)=0.所以,d=0或2a.
S4,即得d (2a-d)=0.所以,d=0或2a.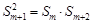 .因此
.因此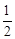 m(m+1)d2=0, ①
m(m+1)d2=0, ①

 黃岡小狀元滿分沖刺微測驗系列答案
黃岡小狀元滿分沖刺微測驗系列答案 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源:不詳 題型:解答題
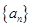 ,
,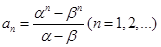 ,其中
,其中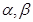 是方程
是方程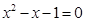 的兩個根.
的兩個根.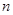 ,都有
,都有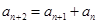 ;
;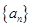 中的項都是正整數,試證明:任意相鄰兩項的最大公約數均為1;
中的項都是正整數,試證明:任意相鄰兩項的最大公約數均為1;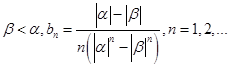 ,證明:
,證明: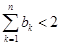 。
。查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 ,我們稱
,我們稱查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 的定義域為R,數列
的定義域為R,數列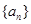 滿足
滿足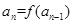 (
(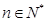 且
且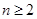 ).
).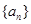 是等差數列,
是等差數列,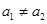 ,且
,且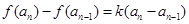 (k為非零常數,
(k為非零常數, 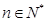 且
且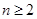 ),求k的值;
),求k的值;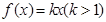 ,
,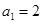 ,
,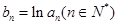 ,數列
,數列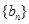 的前n項和為
的前n項和為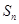 ,對于給定的正整數
,對于給定的正整數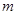 ,如果
,如果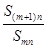 的值與n無關,求k的值.
的值與n無關,求k的值.查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
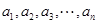 的前k項和為
的前k項和為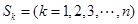 ,定義
,定義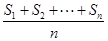 為該項數列的“凱森和”,如果項系數為99項的數列
為該項數列的“凱森和”,如果項系數為99項的數列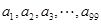 的“凱森和”為1000,那么項數為100的數列100,
的“凱森和”為1000,那么項數為100的數列100,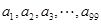 的“凱森和”為( )
的“凱森和”為( )| A.991 | B.1001 | C.1090 | D.1100 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com