
(本小題滿分12分)
如圖所示的幾何體中,四邊形ABCD是等腰梯形,AD//CD,  ,FC
,FC  平面ABCD, AE
平面ABCD, AE  BD,CB =CD=-CF.
BD,CB =CD=-CF.
(Ⅰ)求證:平面ABCD  平面AED;
平面AED;
(Ⅱ)直線AF與面BDF所成角的余弦值
(Ⅰ)見解析 (Ⅱ)
解析試題分析:(Ⅰ)通過計算可證得AD⊥BD,又因為AE⊥BD,由線面垂直的判定定理得,BD⊥面ADE,由面面垂直的判定定理得,面ADE⊥面ABCD; (Ⅱ)由(Ⅰ)知AD⊥BD,同理可證AC⊥BC,因為CF⊥面ABCD,所以以CA,CB,CF分別為 建立空間直角坐標系,設BC=1,求出A、B、D,F點的坐標,求出
建立空間直角坐標系,設BC=1,求出A、B、D,F點的坐標,求出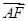 的坐標和平面BDF法向量的坐標,利用空間向量夾角公式計算出這兩個向量夾角的余弦值,利用同腳三角函數基本關系求出向量夾角的正弦值即為線面夾角的余弦值.
的坐標和平面BDF法向量的坐標,利用空間向量夾角公式計算出這兩個向量夾角的余弦值,利用同腳三角函數基本關系求出向量夾角的正弦值即為線面夾角的余弦值.
試題解析:(Ⅰ)∵四邊形ABCD是等腰梯形,AB∥CD,∠DAB=60°,
∴∠ADC=∠BCD=120°,
又CB=CD,∴∠CDB=30°,∴∠ADB=90°,AD⊥BD,
又AE⊥BD,且AE∩AD=A,AE,AD?平面AED,
∴BD⊥平面AED,∴平面ABCD⊥平面AED.
(Ⅱ)連結AC,由(Ⅰ)知AD⊥BD,∴AC⊥BC,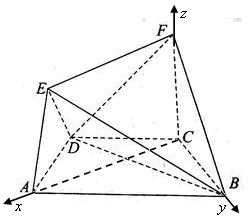
又FC⊥平面ABCD,∴CA,CB,CF兩兩垂直,
以C為坐標原點,建立空間直角坐標系,設CB=1,
則A( ,0,0),B(0,1,0),D(
,0,0),B(0,1,0),D( ,
,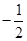 ,0),F(0,0,1),
,0),F(0,0,1),
∴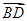 =(
=( ,
,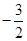 ,0),
,0),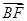 ==(0,?1,1),
==(0,?1,1),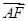 =(-
=(- ,0,1),
,0,1),
設平面BDF的一個法向量為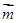 =(x,y,z),則
=(x,y,z),則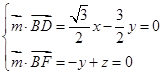 ,取z=1,則
,取z=1,則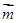 =(
=( ,1,1),
,1,1),
所以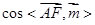 =
=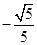 ,∴直線AF與面BDF所成角的余弦值為
,∴直線AF與面BDF所成角的余弦值為 . (12分)
. (12分)
考點:空間線面垂直的判定,空間面面垂直的判定,線面角的計算,推理論證能力,運算求解能力


 每日10分鐘口算心算速算天天練系列答案
每日10分鐘口算心算速算天天練系列答案科目:高中數學 來源: 題型:填空題
下列各命題:
①若直線 ,則
,則 不可能與
不可能與 內無數條直線相交。
內無數條直線相交。
②若平面 內有一條直線和直線
內有一條直線和直線 不共面,則
不共面,則 。
。
③若一個平面內有不共線的三點到另一平面的距離相等,則兩平面平行。
④如果兩個平面垂直,則一個平面內任意直線都和另一個平面垂直。
其中錯誤命題的序號是____________.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,點 為斜三棱柱
為斜三棱柱 的側棱
的側棱 上一點,
上一點,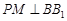 交
交 于點
于點 ,
, 交
交 于點
于點 .
.
(1) 求證: ;
;
(2) 在任意 中有余弦定理:
中有余弦定理: .
.
拓展到空間,類比三角形的余弦定理,寫出斜三棱柱的三個側面面積與其中兩個側面所成的二面角之間的關系式,并予以證明
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,在直三棱柱中 -A BC中,AB
-A BC中,AB 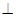 AC, AB=AC=2,
AC, AB=AC=2,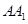 =4,點D是BC的中點.
=4,點D是BC的中點.
(1)求異面直線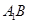 與
與 所成角的余弦值;
所成角的余弦值;
(2)求平面 與
與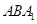 所成二面角的正弦值.
所成二面角的正弦值.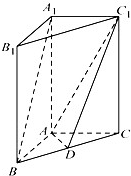
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com