如圖,四邊形

為矩形,

平面
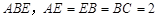
,

為

上的點,且

平面

.
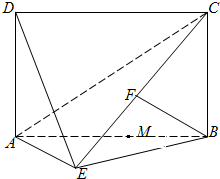
(1)求三棱錐

的體積;
(2)設

在線段

上,且滿足

,試在線段

上確定一點

,使得

平面

.
試題分析:(1)由
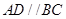
和
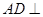
平面
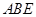
證明
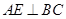
,再由

平面
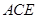
得
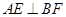
,根據(jù)線面垂直的判定定理證出
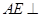
平面
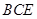
,得出

;由題意知
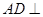
平面
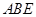
,則過

點作
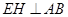
,得到

平面
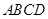
,再根據(jù)條件求出
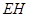
和

,利用換底求出三棱錐的體積;
(2)根據(jù)條件分別在
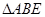
中過
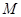
點作
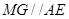
和
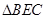
中過
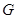
點作

,根據(jù)線面平行的判定證出
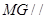
平面

和
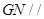
平面

,由面面平行的判定證出平面
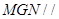
平面

,則得到
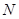
點在線段

上的位置.
試題解析:(1)證明:過

點作
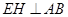
,
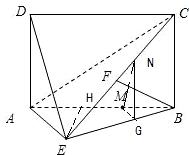
∵
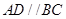
,
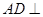
平面
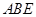
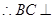
平面
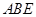
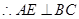
又
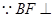
平面
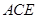
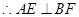

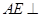
平面
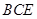
,且
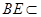
平面
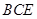
,
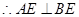
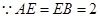
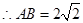
,
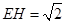

平面
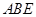
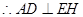
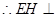
平面
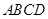
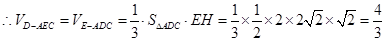
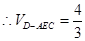
(2)在
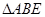
中過
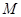
點作
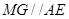
交
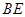
于
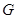
點,在
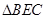
中過
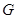
點作

交
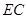
于
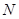
點,連
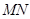
,
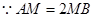
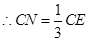
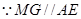
,
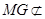
平面

,
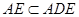
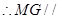
平面

同理可證,
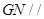
平面

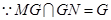
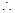
平面
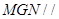
平面

又
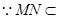
平面
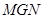
,
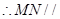
平面

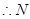
點為線段

上靠近
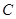
點的一個三等分點
練習冊系列答案
相關習題
科目:高中數(shù)學
來源:不詳
題型:填空題
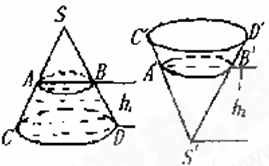
如圖,圓錐形封閉容器,高為h,圓錐內(nèi)水面高為

若將圓錐倒置后,圓錐內(nèi)水面高為
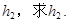
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在四棱錐P-ABCD中,底面ABCD為直角梯形,且AD∥BC,∠ABC=∠PAD=90°,側(cè)面PAD⊥底面ABCD,若PA=AB=BC=
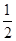
,AD=1.
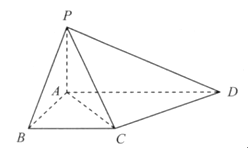
(I)求證:CD⊥平面PAC;
(II)側(cè)棱PA上是否存在點E,使得BE∥平面PCD?若存在,指出點E的位置,并證明,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,六棱錐

的底面是邊長為1的正六邊形,

底面

。
(Ⅰ)求證:平面

平面

;
(Ⅱ)若直線PC與平面PDE所成角的正弦值為
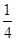
,求六棱錐

高的大小。

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
點(2,3,4)關于x軸的對稱點的坐標為_____
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
如圖,正三棱錐P-ABC的所有棱長都為4.點D,E,F(xiàn)分別在棱PA,PB,PC上,滿足DE=EF=3,DF=2的△DEF個數(shù)是( )
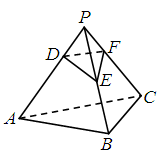
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:單選題
若P是兩條異面直線l,m外的任意一點,則下列命題
①過點P有且只有一條直線與l,m都平行;
②過點P有且只有一條直線與l,m都垂直;
③過點P有且只有一條直線與l,m都相交;
④過點P有且只有一條直線與l,m都異面。
其中假命題的個數(shù)為 ( )
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
集合
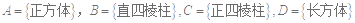
,它們之間的包含關系是
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
在平面幾何中,有這樣一個定理:過三角形的內(nèi)心作一直線,將三角形分成的兩部分的周長比等于其面積比.請你類比寫出在立體幾何中,有關四面體的相似性質(zhì): .
查看答案和解析>>

 為矩形,
為矩形, 平面
平面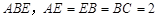 ,
, 為
為 上的點,且
上的點,且 平面
平面 .
. 
 的體積;
的體積; 在線段
在線段 上,且滿足
上,且滿足 ,試在線段
,試在線段 上確定一點
上確定一點 ,使得
,使得 平面
平面 .
.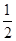 ,AD=1.
,AD=1.
 的底面是邊長為1的正六邊形,
的底面是邊長為1的正六邊形, 底面
底面 。
。 平面
平面 ;
;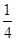 ,求六棱錐
,求六棱錐 高的大小。
高的大小。
