(本小題滿分12分)如圖,正方體ABCD—A
1B
1C
1D
1中,P、M、N分別為棱DD
1、AB、BC的中點 .
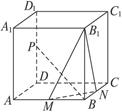
(1)求二面角B
1MNB的正切值;
(2)求證:PB⊥平面MNB
1;
(3)若正方體的棱長為1,畫出一個正方體表面展開圖,使其滿足“有4個正方形面相連成一個長方形”的條件,并求出展開圖中P、B兩點間的距離 .
(1)解:連結(jié)BD交MN于F,連結(jié)B
1F.
∵平面DD
1B
1B⊥平面ABCD,交線為BD,AC⊥BD,
∴AC⊥平面DD
1B
1B.又∵AC//MN,
∴MN⊥平面DD
1B
1B.
∵B
1F,BF

平面DD
1B
1B,
∴B
1F⊥MN,BF⊥MN.
∵B
1F

平面B
1MN,
BF

平面BMN,則∠B
1FB為二面角B
1-MN-B的平面角. -----------------------2分
在Rt△B
1FB中,設(shè)B
1B=1,則FB=

,
∴tan∠B
1FB=

. -------------------------4分
(2)證明:過點P作PE⊥AA
1,則PE∥DA,連結(jié)BE.
又DA⊥平面ABB
1A
1,∴PE⊥平面ABB
1A
1,即PE⊥B
1M.
又BE⊥B
1M,∴B
1M⊥平面PEB.
∴PB⊥MB
1.
由(1)中MN⊥平面DD
1B
1B,得PB⊥MN,所以PB⊥平面MNB
1. -----------------8分
(3)解:PB=

,符合條件的正方體表面展開圖可以是以下6種之一:

-------------12分
試題分析:(1)要求二面角B1-MN-B的正切值,我們要先找出二面角的平面角,再構(gòu)造三角形,解三角形求出其正切值.
(2)要證明PB⊥平面B1MN,我們要在平面內(nèi)找到兩條與PB垂直的相交直線,分析題意可知B1M,B1N滿足要求,進(jìn)而可以轉(zhuǎn)化為證明線線垂直.
(3)利用側(cè)面展開圖來得到BP的長度的求解。
點評:解決該試題的關(guān)鍵是線線垂直可由線面垂直的性質(zhì)推得,直線和平面垂直,這條直線就垂直于平面內(nèi)所有直線,這是尋找線線垂直的重要依據(jù).垂直問題的證明,其一般規(guī)律是“由已知想性質(zhì),由求證想判定”,也就是說,根據(jù)已知條件去思考有關(guān)的性質(zhì)定理;根據(jù)要求證的結(jié)論去思考有關(guān)的判定定理,往往需要將分析與綜合的思路結(jié)合起來.本題也可以用空間向量來解決,其步驟是:建立空間直角坐系⇒明確相關(guān)點的坐標(biāo)⇒明確相關(guān)向量的坐標(biāo)⇒通過空間向量的坐標(biāo)運算求解。
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖幾何體中,四邊形

為矩形,

,
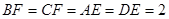
,
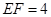
,

,
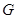
為
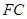
的中點,
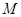
為線段
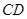
上的一點,且
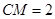
.
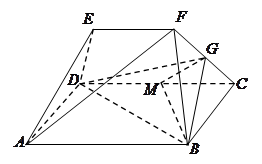
(1)證明:
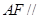
面
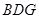
;
(2)證明:面
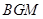
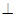
面

;
(3)求三棱錐

的體積
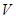
.
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
空間四邊形ABCD的各頂點坐標(biāo)分別是
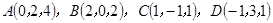
,E,F分別是AB與CD的中點,則EF的長為( )
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:填空題
在空間直角坐標(biāo)系中,已知點A(1,0,2),B(1,—3,1),點M在y軸上,且M到A與到B的距離相等,則M的坐標(biāo)是 。
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
點P(1,2,3)關(guān)于OZ軸的對稱點的坐標(biāo)為( )
| A.(-1, -2, 3) | B.(1, 2, -3) | C.(-1, -2, -3) | D.(-1, 2, -3) |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:解答題
如圖,在四棱錐
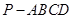
中,
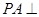
底面
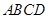
,
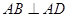
,
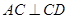
,
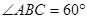
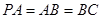
,
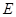
是
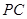
的中點.
(Ⅰ)證明:

;
(Ⅱ)證明:
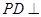
平面
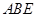
;
(Ⅲ)求二面角
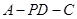
的正切值
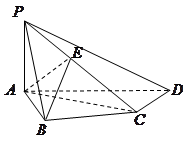
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
(理)已知兩點
M(-1,-6),
N(3,0),點
P(-

,
y)分有向線段

的比為
λ,則
λ,
y的值為( )
查看答案和解析>>


 平面DD1B1B,
平面DD1B1B, 平面B1MN,
平面B1MN, 平面BMN,則∠B1FB為二面角B1-MN-B的平面角. -----------------------2分
平面BMN,則∠B1FB為二面角B1-MN-B的平面角. -----------------------2分 ,
, . -------------------------4分
. -------------------------4分 ,符合條件的正方體表面展開圖可以是以下6種之一:
,符合條件的正方體表面展開圖可以是以下6種之一: -------------12分
-------------12分

 為矩形,
為矩形, ,
,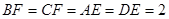 ,
,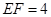 ,
, ,
,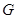 為
為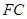 的中點,
的中點, 為線段
為線段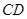 上的一點,且
上的一點,且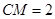 .
.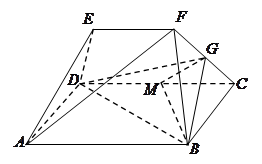
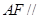 面
面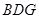 ;
;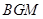
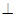 面
面 ;
; 的體積
的體積 .
. ,y)分有向線段
,y)分有向線段 的比為λ,則λ,y的值為( )
的比為λ,則λ,y的值為( ) ,8
,8 ,-8
,-8 ,-8
,-8