
.(本題滿分18分)
本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分8分.
設二次函數 ,對任意實數
,對任意實數 ,有
,有 恒成立;數列
恒成立;數列 滿足
滿足 .
.
(1)求函數 的解析式和值域;
的解析式和值域;
(2)試寫出一個區間 ,使得當
,使得當 時,數列
時,數列 在這個區間上是遞增數列,
在這個區間上是遞增數列,
并說明理由;
(3)已知 ,是否存在非零整數
,是否存在非零整數 ,使得對任意
,使得對任意 ,都有
,都有

 恒成立,若存在,
恒成立,若存在,
求之;若不存在,說明理由.
解:(1)由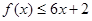 恒成立等價于
恒成立等價于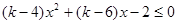 恒成立……1分
恒成立……1分
從而得: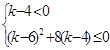 ,化簡得
,化簡得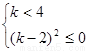 ,從而得
,從而得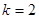 ,
,
所以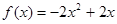 ,………3分
,………3分
其值域為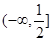 .………………………………………………4分
.………………………………………………4分
(2)解:當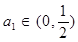 時,數列
時,數列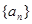 在這個區間上是遞增數列,證明如下:
在這個區間上是遞增數列,證明如下:
設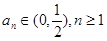 ,則
,則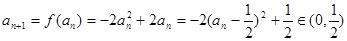 ,
,
所以對一切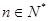 ,均有
,均有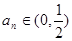 ;………………………………………7分
;………………………………………7分
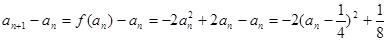
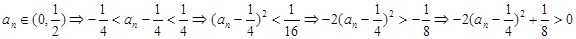 ,從而得
,從而得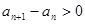 ,即
,即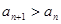 ,
,
所以數列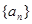 在區間
在區間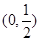 上是遞增數列.………10分
上是遞增數列.………10分
注:本題的區間也可以是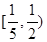 、
、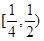 、
、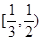 等無窮多個.
等無窮多個.
另解:若數列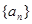 在某個區間上是遞增數列,則
在某個區間上是遞增數列,則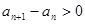
即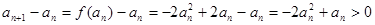
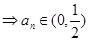 …7分
…7分
又當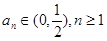 時,
時,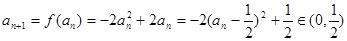 ,
,
所以對一切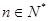 ,均有
,均有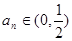 且
且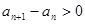 ,
,
所以數列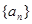 在區間
在區間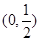 上是遞增數列.…………………10分
上是遞增數列.…………………10分
(3)(文科)由(2)知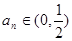 ,從而
,從而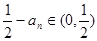 ;
;
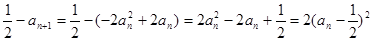 ,
,
即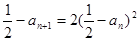 ; ………12分
; ………12分
令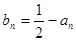 ,則有
,則有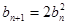 且
且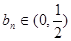 ;
;
從而有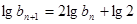 ,可得
,可得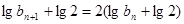 ,所以數列
,所以數列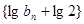 是以
是以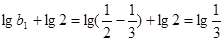 為首項,公比為
為首項,公比為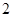 的等比數列,……14分
的等比數列,……14分
從而得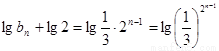 ,即
,即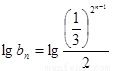 ,
,
所以 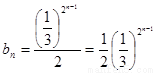 ,
,
所以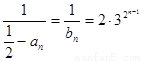 ,
,
所以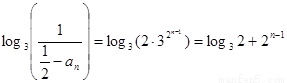 , ………………16分
, ………………16分
所以,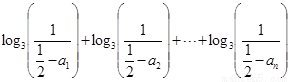
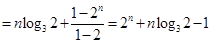 .
………………………18分
.
………………………18分
(3)(理科)由(2)知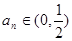 ,從而
,從而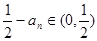 ;
;
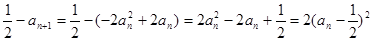 ,
,
即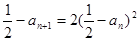 ;………12分
;………12分
令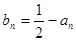 ,則有
,則有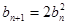 且
且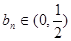 ;
;
從而有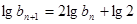 ,可得
,可得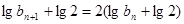 ,所以數列
,所以數列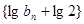 是
是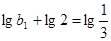 為首項,公比為
為首項,公比為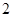 的等比數列,………………………14分
的等比數列,………………………14分
從而得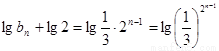 ,即
,即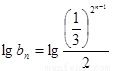 ,
,
所以 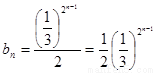 ,
,
所以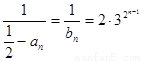 ,所以
,所以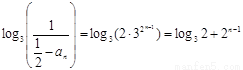 ,
,
所以,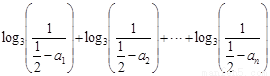
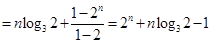 .…………………………16分
.…………………………16分
即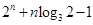
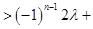
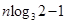 ,所以,
,所以,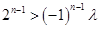 恒成立
恒成立
當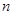 為奇數時,即
為奇數時,即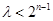 恒成立,當且僅當
恒成立,當且僅當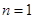 時,
時,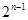 有最小值
有最小值 為。
為。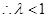
當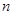 為偶數時,即
為偶數時,即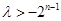 恒成立,當且僅當
恒成立,當且僅當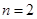 時,有最大值
時,有最大值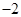 為。
為。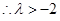 [
[
∴,對任意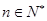 ,有
,有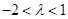 。又
。又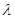 非零整數,
非零整數,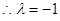 ……………18分
……………18分
【解析】略


科目:高中數學 來源: 題型:
(本題滿分18分,第(1)小題6分,第(2)小題6分,第(3)小題6分)
若數列![]() 滿足:
滿足:![]() 是常數),則稱數列
是常數),則稱數列![]() 為二階線性遞推數列,且定義方程
為二階線性遞推數列,且定義方程![]() 為數列
為數列![]() 的特征方程,方程的根稱為特征根; 數列
的特征方程,方程的根稱為特征根; 數列![]() 的通項公式
的通項公式![]() 均可用特征根求得:
均可用特征根求得:
①若方程![]() 有兩相異實根
有兩相異實根![]() ,則數列通項可以寫成
,則數列通項可以寫成![]() ,(其中
,(其中![]() 是待定常數);
是待定常數);
②若方程![]() 有兩相同實根
有兩相同實根![]() ,則數列通項可以寫成
,則數列通項可以寫成![]() ,(其中
,(其中![]() 是待定常數);
是待定常數);
再利用![]() 可求得
可求得![]() ,進而求得
,進而求得![]() .
.
根據上述結論求下列問題:
(1)當![]() ,
,![]() (
(![]() )時,求數列
)時,求數列![]() 的通項公式;
的通項公式;
(2)當![]() ,
,![]() (
(![]() )時,求數列
)時,求數列![]() 的通項公式;
的通項公式;
(3)當![]() ,
,![]() (
(![]() )時,記
)時,記![]() ,若
,若![]() 能被數
能被數![]() 整除,求所有滿足條件的正整數
整除,求所有滿足條件的正整數![]() 的取值集合.
的取值集合.
查看答案和解析>>
科目:高中數學 來源:2011屆上海市盧灣區高三上學期期末數學理卷 題型:解答題
(本題滿分18分)本題共有3個小題,第1小題滿分4分,第2小題滿分8分,第3小題滿分6分.
已知負數 和正數
和正數 ,且對任意的正整數n,當
,且對任意的正整數n,當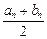 ≥0時, 有[
≥0時, 有[ ,
,  ]=
]=
[ ,
, 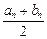 ];當
];當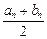 <0時, 有[
<0時, 有[ ,
,  ]= [
]= [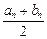 ,
, 
 ].
].
(1)求證數列{ }是等比數列;
}是等比數列;
(2)若 ,求證
,求證
 ;
;
(3)是否存在 ,使得數列
,使得數列 為常數數列?請說明理由
為常數數列?請說明理由
查看答案和解析>>
科目:高中數學 來源:2011-2012學年山東省濟寧市高三第二次月考文科數學 題型:解答題
(本題滿分18分)已知拋物線C的頂點在原點,焦點在y軸正半軸上,點 到其準線的距離等于5.
到其準線的距離等于5.
(Ⅰ)求拋物線C的方程;
(Ⅱ)如圖,過拋物線C的焦點的直線從左到右依次與拋物線C及圓 交于A、C、D、B四點,試證明
交于A、C、D、B四點,試證明 為定值;
為定值;
(Ⅲ)過A、B分別作拋物C的切線 且
且 交于點M,求
交于點M,求 與
與 面積之和的最小值.
面積之和的最小值.

查看答案和解析>>
科目:高中數學 來源:2011-2012學年上海市青浦區高三上學期期終學習質量調研測試數學試卷 題型:解答題
(本題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分,第3小題滿分8分.
設 ,對于項數為
,對于項數為 的有窮數列
的有窮數列 ,令
,令 為
為 中最大值,稱數列
中最大值,稱數列 為
為 的“創新數列”.例如數列
的“創新數列”.例如數列 3,5,4,7的創新數列為3,5,5,7.
3,5,4,7的創新數列為3,5,5,7.
考查自然數 的所有排列,將每種排列都視為一個有窮數列
的所有排列,將每種排列都視為一個有窮數列 .
.
(1)若 ,寫出創新數列為3,4,4,4的所有數列
,寫出創新數列為3,4,4,4的所有數列 ;
;
(2)是否存在數列 的創新數列為等比數列?若存在,求出符合條件的創新數列;若不存在,請說明理由.
的創新數列為等比數列?若存在,求出符合條件的創新數列;若不存在,請說明理由.
(3)是否存在數列 ,使它的創新數列為等差數列?若存在,求出滿足所有條件的數列
,使它的創新數列為等差數列?若存在,求出滿足所有條件的數列 的個數;若不存在,請說明理由.
的個數;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源:上海市普陀區2010屆高三第二次模擬考試數學文 題型:解答題
(本題滿分18分,其中第1小題6分,第2小題6分,第3小題6分)
已知數列 的首項為1,前
的首項為1,前 項和為
項和為 ,且滿足
,且滿足 ,
, .數列
.數列 滿足
滿足 .
.
(1) 求數列 的通項公式;
的通項公式;
(2) 當 時,試比較
時,試比較 與
與 的大小,并說明理由;
的大小,并說明理由;
(3) 試判斷:當 時,向量
時,向量
 是否可能恰為直線
是否可能恰為直線
 的方向向量?請說明你的理由.
的方向向量?請說明你的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com