
 | 0.010 | 0.005 | 0.001 |
 | 6.635 | 7.879 | 10.828 |

 .
. 的值進行數據比較得出結論;(Ⅱ)根據題意可知X的分布滿足二項分布X~B(3,
的值進行數據比較得出結論;(Ⅱ)根據題意可知X的分布滿足二項分布X~B(3, ),利用二項分布的公式直接求解.
),利用二項分布的公式直接求解.| | 語文優秀 | 語文不優秀 | 總計 |
| 外語優秀 | 60 | 100 | 160 |
| 外語不優秀 | 140 | 500 | 640 |
| 總計 | 200 | 600 | 800 |
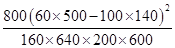 ≈16.667>10.828,
≈16.667>10.828, .
. ),P(X=k)=
),P(X=k)= (
( )k(
)k( )8-k,k=0,1,2,3.
)8-k,k=0,1,2,3.| X | 0 | 1 | 2 | 3 |
| p | 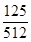 |  |  |  |
 =
= .
.

 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:高中數學 來源:不詳 題型:解答題
| 男 | | 女 | ||||||
| | | 8 | 16 | 5 | 8 | 9 | | |
| 8 | 7 | 6 | 17 | 2 | 3 | 5 | 5 | 6 |
| 7 | 4 | 2 | 18 | 0 | 1 | 2 | | |
| | | 1 | 19 | 0 | | | | |
 表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出
表示所選志愿者中能擔任“禮儀小姐”的人數,試寫出 的分布列,并求
的分布列,并求 的數學期望.
的數學期望.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 戶家庭,分別調查了他們在政府動員前后三個月的月平均用水量(單位:噸),將所得數據分組,畫出頻率分布直方圖(如圖所示)
戶家庭,分別調查了他們在政府動員前后三個月的月平均用水量(單位:噸),將所得數據分組,畫出頻率分布直方圖(如圖所示)

 戶,在政府進行節水動員前平均每月用水量是
戶,在政府進行節水動員前平均每月用水量是 噸,請估計該小區在政府動員后比動員前平均每月節約用水多少噸;
噸,請估計該小區在政府動員后比動員前平均每月節約用水多少噸; 范圍內的家庭中選出
范圍內的家庭中選出 戶作為采訪對象,其中在
戶作為采訪對象,其中在 內的抽到
內的抽到 戶,求
戶,求 的分布列和期望
的分布列和期望 查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 的分布列和數學期望.
的分布列和數學期望. 查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 內,不等式
內,不等式 確定的平面區域為
確定的平面區域為 ,不等式組
,不等式組 確定的平面區域為
確定的平面區域為 .
. 中任取3個“整點”,求這些“整點”中恰好有2個“整點”落在區域
中任取3個“整點”,求這些“整點”中恰好有2個“整點”落在區域 中的概率;
中的概率; 中每次任取一個點,連續取3次,得到3個點,記這3個點落在區域
中每次任取一個點,連續取3次,得到3個點,記這3個點落在區域 中的個數為
中的個數為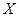 ,求
,求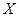 的分布列和數學期望.
的分布列和數學期望.查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
 (元)的概率分布列和期望
(元)的概率分布列和期望 .
.查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
 表示小李同學首先摸到黃色乒乓球時的摸球次數,則隨機變量
表示小李同學首先摸到黃色乒乓球時的摸球次數,則隨機變量 的數學期望值
的數學期望值 .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com