中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

（1）求數列的通項公式；
（2）求數列的前n項和；
（3）令，求數列的前n項和。
解：（1）因為，所以，
所以。
（2）；
（3）因為，
所以。
練習冊系列答案
相關習題

科目：高中數學 來源： 題型：

已知等差數列的定義為：在一個數列中，從第二項起，如果每一項與它的前一項的差都為同一個常數，那么這個數列叫做等差數列，這個常數叫做該數列的公差．
（1）類比等差數列的定義給出“等和數列”的定義；
（2）已知數列{an}是等和數列，且a1=2，公和為5，求 a18的值，并猜出這個數列的通項公式（不要求證明）．

查看答案和解析>>

科目：高中數學 來源： 題型：

已知數列{an}中，a1=1，Sn是數列{an}的前n項和，且滿足：2Sn+1+an+1+4Sn+1Sn=0，
（1）求數列{an}的通項公an
（2）若記bn=(2n+1)•(
1Sn
+2)，Tn為數列{bn}的前n項和，求Tn．

查看答案和解析>>

科目：高中數學 來源：2010年揚州中學高二下學期期末考試數學 題型：解答題

(14分) 已知等差數列的定義為:在一個數列中，從第二項起,如果每一項與它的前一項的差都為同一個常數，那么這個數列叫做等差數列，這個常數叫做該數列的公差．（1）類比等差數列的定義給出“等和數列”的定義；（2） 已知數列是等和數列，且，公和為，求 的值，并猜出這個數列的通項公式(不要求證明)。

查看答案和解析>>

科目：高中數學 來源：2013屆黑龍江虎林高中高二下學期期中理科數學試卷（解析版） 題型：解答題

數列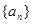，滿足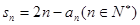

（1）求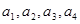，并猜想通項公式。

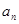（2）用數學歸納法證明（1）中的猜想。

【解析】本試題主要考查了數列的通項公式求解，并用數學歸納法加以證明。第一問利用遞推關系式得到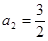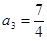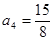，，，，并猜想通項公式

第二問中，用數學歸納法證明（1）中的猜想。

①對n=1，等式成立。

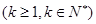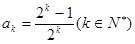②假設n=k時，成立，

那么當n=k+1時，

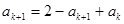，所以當n=k+1時結論成立可證。

數列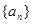，滿足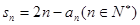

（1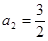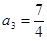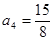），，，并猜想通項公。  …4分

（2）用數學歸納法證明（1）中的猜想。①對n=1，等式成立。  …5分

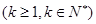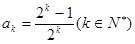②假設n=k時，成立，

那么當n=k+1時，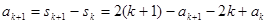

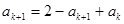，             ……9分

所以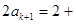

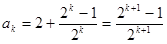
所以當n=k+1時結論成立                     ……11分

由①②知，猜想對一切自然數n均成立

 

查看答案和解析>>

科目：高中數學 來源：2009-2010學年江蘇省揚州中學高二（下）期末數學試卷（解析版） 題型：填空題

已知等差數列的定義為：在一個數列中，從第二項起，如果每一項與它的前一項的差都為同一個常數，那么這個數列叫做等差數列，這個常數叫做該數列的公差．
（1）類比等差數列的定義給出“等和數列”的定義；
（2）已知數列{an}是等和數列，且a1=2，公和為5，求 a18的值，并猜出這個數列的通項公式（不要求證明）．

查看答案和解析>>

同步練習冊答案