
(本小題滿分14分)
一個幾何體是由圓柱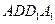 和三棱錐
和三棱錐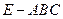 組合而成,點
組合而成,點 、
、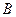 、
、 在圓
在圓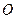 的圓周上,其正(主)視圖、側(左)視圖的面積分別為10和12,如圖3所示,其中
的圓周上,其正(主)視圖、側(左)視圖的面積分別為10和12,如圖3所示,其中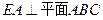 ,
,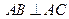 ,
,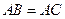 ,
,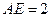 .
.
(1)求證: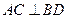 ;
;
(2)求二面角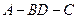 的平面角的大小.
的平面角的大小.
方法1:(1)證明:因為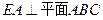 ,
,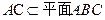 ,所以
,所以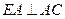 ,即
,即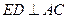 .
.
又因為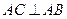 ,
,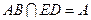 ,所以
,所以 平面
平面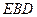 .
.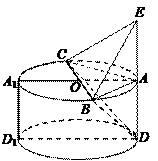
因為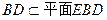 ,所以
,所以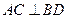 .………………………………………4分
.………………………………………4分
(2)解:因為點 、
、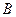 、
、 在圓
在圓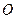 的圓周上,且
的圓周上,且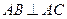 ,所以
,所以 為圓
為圓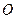 的直徑.
的直徑.
設圓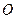 的半徑為
的半徑為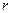 ,圓柱高為
,圓柱高為 ,根據正(主)視圖、側(左)視圖的面積可得,
,根據正(主)視圖、側(左)視圖的面積可得,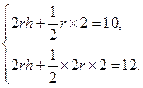 …………………………………………6分
…………………………………………6分
解得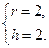
所以 ,
,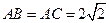 .…………………………………………………………………7分
.…………………………………………………………………7分
過點 作
作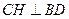 于點
于點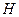 ,連接
,連接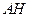 ,
,
由(1)知,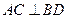 ,
,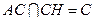 ,所以
,所以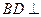 平面
平面 .
.
因為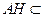 平面
平面 ,所以
,所以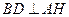 .
.
所以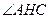 為二面角
為二面角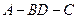 的平面角.………………………………9分
的平面角.………………………………9分
由(1)知, 平面
平面 ,
,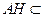 平面
平面 ,
,
所以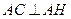 ,即△
,即△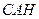 為直角三角形.
為直角三角形.
在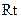 △
△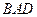 中,
中, ,
,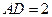 ,則
,則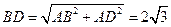 .
.
由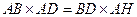 ,解得
,解得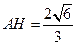 .
.
因為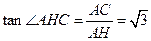 .………………………………………………………13分
.………………………………………………………13分
所以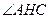
 .
.
所以二面角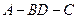 的平面角大小為
的平面角大小為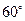 .………………………………14分
.………………………………14分
方法2:(1)證明:因為點 、
、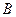 、
、 在圓
在圓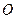 的圓周上,且
的圓周上,且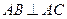 ,所以
,所以 為圓
為圓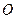 的直徑.
的直徑.
設圓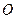 的半徑為
的半徑為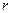 ,圓柱高為
,圓柱高為 ,根據正(主)視圖、側(左)視圖的面積可得,
,根據正(主)視圖、側(左)視圖的面積可得,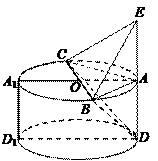
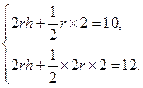 …………………………………………2分
…………………………………………2分
解得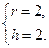
所以 ,
,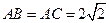
解析


科目:高中數學 來源: 題型:解答題
(本小題滿分14分).如圖,在三棱錐P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,點D、E分別在棱PB、PC的中點,且DE∥BC.
(1)求證:DE∥平面ACD
(2)求證:BC⊥平面PAC;
(3)求AD與平面PAC所成的角的正弦值;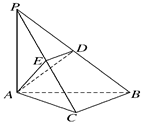
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
如圖,在梯形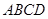 中,
中,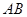 ∥
∥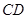 ,
,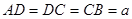 ,
,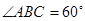 ,平面
,平面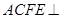 平面
平面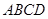 ,四邊形
,四邊形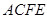 是矩形,
是矩形,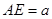 ,點
,點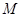 在線段
在線段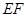 上.
上.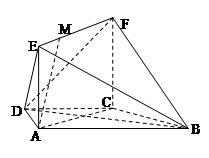
(1)求證:平面BCF⊥平面ACFE;
(2)當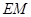 為何值時,
為何值時,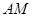 ∥平面
∥平面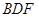 ?證明你的結論;
?證明你的結論;
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,已知圓錐的軸截面ABC是邊長為2的正三角形,O是底面圓心.
(Ⅰ)求圓錐的表面積;
(Ⅱ)經過圓錐的高AO的中點O¢作平行于圓錐底面的截面,
求截得的圓臺的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如右圖所示,在正三棱柱ABC—A1B1C1中,AB=3,AA1=4,M為AA1的中點,P是BC上一點,且由P沿棱柱側面經過棱CC1到M的最短路線長為,設這條最短路線與CC1的交點為N.求: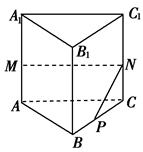
(1)該三棱柱的側面展開圖的對角線長;
(2)PC和NC的長.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題滿分12分)
如圖,四邊形ABCD為正方形,四邊形BDEF為矩形,AB=2BF,E丄平面ABCD,G為EF中點.
(1)求證:CF//平面
(2) 求證:平面ASG丄平面CDG;
(3)求二面角C—FG—B的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(本小題13分)
一個用鮮花做成的花柱,它的下面是一個直徑為2m、高為4m的圓柱形物體,上面是一個直 徑為2m的半球形體,如果每平方米大約需要鮮花200朵,那么裝飾這個花柱大約需要多少朵鮮花(
徑為2m的半球形體,如果每平方米大約需要鮮花200朵,那么裝飾這個花柱大約需要多少朵鮮花(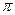 取3.1)?
取3.1)?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com