
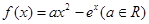 .
.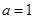 時,試判斷
時,試判斷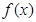 的單調性并給予證明;
的單調性并給予證明;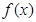 有兩個極值點
有兩個極值點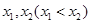 .
.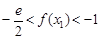 。 (注:
。 (注: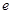 是自然對數的底數)
是自然對數的底數)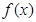 在R上單調遞減 (2)
在R上單調遞減 (2)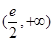 ,對于函數中不等式的證明,一般要功過構造函數來結合函數的最值來證明不等式的成立。
,對于函數中不等式的證明,一般要功過構造函數來結合函數的最值來證明不等式的成立。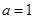 時,
時,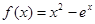 ,
,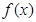 在R上單調遞減 …………1分
在R上單調遞減 …………1分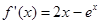 ,只要證明
,只要證明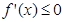 恒成立, …………………………2分
恒成立, …………………………2分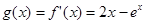 ,則
,則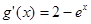 ,
,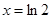 時,
時,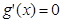 ,
,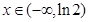 時,
時,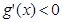 ,當
,當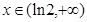 時,
時,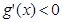 ………………4分
………………4分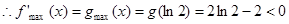 ,故
,故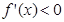 恒成立
恒成立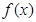 在R上單調遞減 ……………………6分
在R上單調遞減 ……………………6分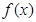 有兩個極值點
有兩個極值點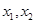 ,則
,則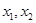 是方程
是方程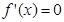 的兩個根,
的兩個根,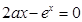 有兩個根
有兩個根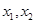 ,
,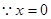 顯然不是該方程的根,所以方程
顯然不是該方程的根,所以方程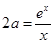 有兩個根, …………8分
有兩個根, …………8分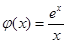 ,得
,得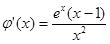
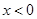 時,
時,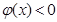 且
且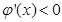 ,
,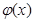 單調遞減
單調遞減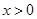 時,
時,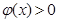
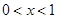 時
時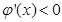 ,
,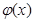 單調遞減
單調遞減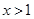 時
時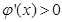 ,
,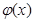 單調遞增 ……………………………10分
單調遞增 ……………………………10分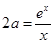 有兩個根,需
有兩個根,需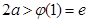 ,故
,故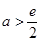 且
且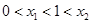
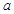 的取值范圍為
的取值范圍為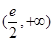 ……………………………………12分
……………………………………12分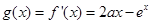 ,則
,則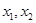 是方程
是方程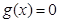 的兩個根,
的兩個根,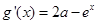 ,
,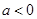 時,
時,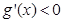 恒成立,
恒成立,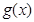 單調遞減,方程
單調遞減,方程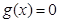 不可能有兩個根
不可能有兩個根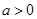 ,由
,由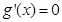 ,得
,得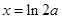 ,
,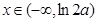 時,
時,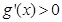 ,當
,當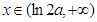 時,
時,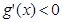
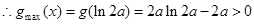 ,得
,得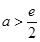
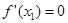 ,得:
,得: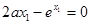 ,故
,故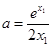 ,
,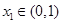
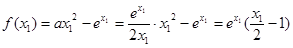 ,
,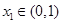 ………………14分
………………14分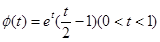 ,則
,則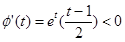 ,
,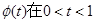 上單調遞減
上單調遞減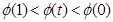 ,即
,即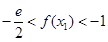 ………………………………15分
………………………………15分

 閱讀快車系列答案
閱讀快車系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com