
(本題滿分12分)某民營企業生產A、B兩種產品,根據市場調查和預測,A產品的利潤y與投資額x成正比,其關系如圖1所示;B產品的利潤y與投資額x的算術平方根成正比,其關系如圖2所示(利潤與投資額的單位均為萬元). (1)分別將A、B兩種產品的利潤表示為投資額的函數關系式;(2)該企業已籌集到10萬元資金,并全部投入A、B兩種產品的生產,問:怎樣分配這10萬元投資,才能使企業獲得最大利潤,其最大利潤為多少萬元?
(1)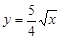 (
(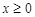 ).
).
(2)A產品投資3.75 萬元,B產品投資 6.25 萬元,才能使企業獲得最大利潤.最大利潤為 4.0625 萬元.
【解析】
試題分析:(1)依題意,A產品的利潤y與投資額x的函數關系式設為 y=kx,(k為參數)
由圖形知,當x=1.8時,y=0.45,代入得k=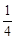 .所以函數關系式為
.所以函數關系式為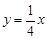 (
(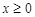 ). 3分
). 3分
B產品的利潤y與投資額x的函數關系式設為  (
(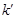 為參數),
為參數),
由圖形知,當x=4時,y=2.5,代入得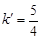 .所以函數關系式為
.所以函數關系式為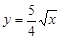 (
(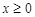 ).6分
).6分
(2)設B產品投資x萬元,則A產品投資(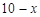 )萬元.
)萬元.
依題意總利潤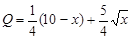 (
(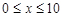 )
8分
)
8分
=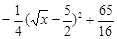
當 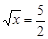 時, 即
時, 即
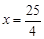 時, Q有最大值
時, Q有最大值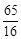 11分
11分
答:A產品投資3.75 萬元,B產品投資 6.25 萬元,才能使企業獲得最大利潤.最大利潤為 4.0625 萬元.---------- 12分
考點:本題主要考查函數模型,二次函數的圖象和性質。
點評:典型題,學習數學的重要意義是應用。本題以企業生產經營為背景,通過構建函數模型,并利用換元法轉化成二次函數問題,研究最大利潤的獲取情況。


科目:高中數學 來源: 題型:
(本題滿分12分)
某校從參加高一年級期中考試的學生中隨機抽出![]() 名學生,將其數學成績(均為整數)分成六段
名學生,將其數學成績(均為整數)分成六段![]() ,
,![]() …
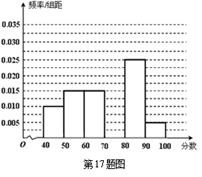
…![]() 后得到如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
后得到如下部分頻率分布直方圖.觀察圖形的信息,回答下列問題:
(Ⅰ)求分數在![]() 內的頻率,并補全這個頻率分布直方圖;
內的頻率,并補全這個頻率分布直方圖;
(Ⅱ)統計方法中,同一組數據常用該組區間的中點值作為代表,據此估計本次考試的平均分;
(Ⅲ)若從![]() 名學生中隨機抽取
名學生中隨機抽取![]() 人,抽到的學生成績在
人,抽到的學生成績在![]() 記
記![]() 分,在
分,在![]() 記
記![]() 分,在
分,在![]() 記
記![]() 分,用
分,用![]() 表示抽取結束后的總記分,求
表示抽取結束后的總記分,求![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源:2011屆四川省南充市高三適應性考試數學理卷 題型:解答題
(本題滿分12分)
某單位6個員工借助互聯網開展工作,每個員工上網的概率都是0.5,且相互之間無影響.
(1)求至少3個員工同時上網的概率;
(2)求至少幾個員工同時上網的概率小于0.3?
查看答案和解析>>
科目:高中數學 來源:2014屆湖北省高二上學期期中考試理科數學試卷(解析版) 題型:解答題
(本題滿分12分)某校從高二年級學生中隨機抽取60名學生,將其期中考試的政治成績(均為整數)分成六段:
 ,
, ,…,
,…, 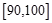 后得到如下頻率分布直方圖.
后得到如下頻率分布直方圖.

(Ⅰ)求分數在 內的頻率;
內的頻率;
(Ⅱ)用分層抽樣的方法在80分以上(含80分)的學生中抽取一個容量為6的樣本,將該樣 本看成一個總體,從中任意選取2人, 求其中恰有1人的分數不低于90分的概率.
查看答案和解析>>
科目:高中數學 來源:2014屆云南省高二上學期期中考試理科數學試卷(解析版) 題型:解答題
(本題滿分12分)某廠生產 兩型會議桌,每套會議桌需經過加工木材和上油漆兩道工序才能完成。已知做一套
兩型會議桌,每套會議桌需經過加工木材和上油漆兩道工序才能完成。已知做一套 型會議桌需要加工木材的時間分別為1小時和2小時,上油漆需要的時間分別為3小時和1小時。廠里規定:加工木材的時間每天不得超過8小時,上油漆的時間每天不得超過9小時。已知該廠生產一套
型會議桌需要加工木材的時間分別為1小時和2小時,上油漆需要的時間分別為3小時和1小時。廠里規定:加工木材的時間每天不得超過8小時,上油漆的時間每天不得超過9小時。已知該廠生產一套 型會議桌分別可獲得利潤2千元和3千元,試問:該廠每天應分別生產
型會議桌分別可獲得利潤2千元和3千元,試問:該廠每天應分別生產 兩型會議桌多少套,才能獲得最大利潤?最大利潤是多少?
兩型會議桌多少套,才能獲得最大利潤?最大利潤是多少?
查看答案和解析>>
科目:高中數學 來源:2010年陜西省高二上學期期中考試數學理卷 題型:解答題
(本題滿分12分)某學校校辦工廠有毀壞的房屋一座,留有一面14m的舊墻,現準備利用這面墻的一段為面墻,建造平面圖形為矩形且面積為126 的廠房(不管墻高),工程的造價是:
的廠房(不管墻高),工程的造價是:
(1)修1m舊墻的費用是造1m新墻費用的25%;
(2)拆去1m舊墻用所得的材料來建1m新墻的費用是建1m新墻費用的50%.
問如何利用舊墻才能使建墻的費用最低?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com