
已知函數f(x)= x3-x2+ax-a(a∈R).
x3-x2+ax-a(a∈R).
(1)當a=-3時,求函數f(x)的極值.
(2)若函數f(x)的圖象與x軸有且只有一個交點,求a的取值范圍.
(1) 當x=-1時,函數f(x)取得極大值為f(-1)=-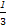 -1+3+3=
-1+3+3=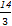 ,
,
當x=3時,函數f(x)取得極小值為f(3)=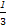 ×27-9-9+3=-6.
×27-9-9+3=-6.
(2) (0,+∞)
【解析】(1)當a=-3時,f(x)=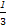 x3-x2-3x+3.
x3-x2-3x+3.
f'(x)=x2-2x-3=(x-3)(x+1).
令f'(x)=0,得x1=-1,x2=3.
當x<-1時,f'(x)>0,
則函數在(-∞,-1)上是增函數,
當-1<x<3時,f'(x)<0,
則函數在(-1,3)上是減函數,
當x>3時,f'(x)>0,
則函數在(3,+∞)上是增函數.
所以當x=-1時,函數f(x)取得極大值為f(-1)=-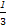 -1+3+3=
-1+3+3=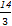 ,
,
當x=3時,函數f(x)取得極小值為f(3)=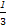 ×27-9-9+3=-6.
×27-9-9+3=-6.
(2)因為f'(x)=x2-2x+a,
所以Δ=4-4a=4(1-a).
①當a≥1時,則Δ≤0,∴f'(x)≥0在R上恒成立,所以f(x)在R上單調遞增.
f(0)=-a<0,f(3)=2a>0,所以,當a≥1時函數的圖象與x軸有且只有一個交點.
②a<1時,則Δ>0,∴f'(x)=0有兩個不等實數根,不妨設為x1,x2(x1<x2),∴x1+x2=2,x1·x2=a,
則
x | (-∞,x1) | x1 | (x1,x2) | x2 | (x2,+∞) |
f'(x) | + | 0 | - | 0 | + |
f(x) | ↗ | 極大值 | ↘ | 極小值 | ↗ |
∵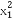 -2x1+a=0,∴a=-
-2x1+a=0,∴a=-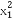 +2x1,
+2x1,
∴f(x1)= -
-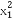 +ax1-a
+ax1-a
= -
-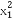 +ax1+
+ax1+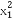 -2x1
-2x1
= +(a-2)x1
+(a-2)x1
=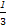 x1[
x1[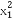 +3(a-2)],
+3(a-2)],
同理f(x2)=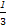 x2[
x2[ +3(a-2)].
+3(a-2)].
∴f(x1)·f(x2)=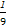 x1x2[
x1x2[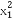 +3(a-2)][
+3(a-2)][ +3(a-2)]=
+3(a-2)]= a(a2-3a+3).
a(a2-3a+3).
令f(x1)·f(x2)>0,解得a>0.
而當0<a<1時,f(0)=-a<0,f(3)=2a>0.
故0<a<1時,函數f(x)的圖象與x軸有且只有一個交點.
綜上所述,a的取值范圍是(0,+∞).


科目:高中數學 來源:2014年高考數學全程總復習課時提升作業四十 第六章第六節練習卷(解析版) 題型:解答題
某同學在一次研究性學習中發現,以下五個式子的值都等于同一個常數.
(1)sin213°+cos217°-sin 13°cos 17°.
(2)sin215°+cos215°-sin 15°cos 15°.
(3)sin218°+cos212°-sin 18°cos 12°.
(4)sin2(-18°)+cos248°-sin(-18°)cos 48°.
(5)sin2(-25°)+cos255°-sin(-25°)cos 55°.
①試從上述五個式子中選擇一個,求出這個常數.
②根據①的計算結果,將該同學的發現推廣為三角恒等式,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業十八第三章第二節練習卷(解析版) 題型:選擇題
在△ABC中,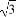 sin(
sin(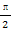 -A)=3sin(π-A),且cosA=-
-A)=3sin(π-A),且cosA=-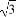 cos(π-B),則C等于( )
cos(π-B),則C等于( )
(A) (B)
(B) (C)
(C)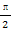 (D)
(D)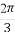
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業十五第二章第十二節練習卷(解析版) 題型:填空題
已知f(x)=x3-3x+m在區間[0,2]上任取三個不同的數a,b,c,均存在以f(a),f(b),f(c)為邊長的三角形,則m的取值范圍是 .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業十五第二章第十二節練習卷(解析版) 題型:選擇題
設f(x),g(x)在[a,b]上可導,且f′(x)>g′(x),則當a<x<b時,有( )
(A)f(x)>g(x)
(B)f(x)<g(x)
(C)f(x)+g(a)>g(x)+f(a)
(D)f(x)+g(b)>g(x)+f(b)
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業十九第三章第三節練習卷(解析版) 題型:填空題
已知直線y=b(b<0)與曲線f(x)=sin(2x+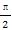 )在y軸右側依次的前三個交點的橫坐標成等比數列,則b的值是 .
)在y軸右側依次的前三個交點的橫坐標成等比數列,則b的值是 .
查看答案和解析>>
科目:高中數學 來源:2014年高考數學全程總復習課時提升作業十七第三章第一節練習卷(解析版) 題型:選擇題
若sinθcosθ>0,則θ在( )
(A)第一、二象限 (B)第一、三象限
(C)第一、四象限 (D)第二、四象限
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com