設函數f(x)＝x＋ax2＋bln x，曲線y＝f(x)在點P(1,0)處的切線斜率為2.
(1)求a，b的值；
(2)證明：f(x)≤2x－2.
計算高手系列答案科目：高中數學 來源： 題型：解答題
已知函數f(x)=ax3+3x2-6ax-11,g(x)=3x2+6x+12和直線m:y=kx+9,且f′(-1)=0.
(1)求a的值.
(2)是否存在k的值,使直線m既是曲線y=f(x)的切線,又是曲線y=g(x)的切線?如果存在,求出k的值;如果不存在,說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝aln x＝
(a為常數)．
(1)若曲線y＝f(x)在點(1，f(1))處的切線與直線x＋2y－5＝0垂直，求a的值；
(2)求函數f(x)的單調區間；
(3)當x≥1時，f(x)≤2x－3恒成立，求a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝x2＋xsin x＋cos x.
(1)若曲線y＝f(x)在點(a，f(a))處與直線y＝b相切，求a與b的值；
(2)若曲線y＝f(x)與直線y＝b有兩個不同交點，求b的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝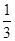
ax3－
x2＋cx＋d(a，c，d∈R)滿足f(0)＝0，f′(1)＝0，且f′(x)≥0在R上恒成立．
(1)求a，c，d的值；
(2)若h(x)＝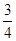
x2－bx＋
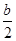－，解不等式f′(x)＋h(x)<0.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數
在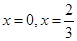
處存在極值.
(1)求實數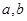
的值；
(2)函數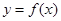
的圖像上存在兩點A，B使得
是以坐標原點O為直角頂點的直角三角形，且斜邊AB的中點在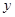
軸上，求實數
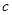的取值范圍；
(3)當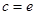
時，討論關于
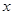的方程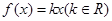
的實根個數.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知函數f(x)＝ex－kx2，x∈R.
(1)若k＝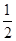
，求證：當x∈(0，＋∞)時，f(x)>1；
(2)若f(x)在區間(0，＋∞)上單調遞增，試求k的取值范圍；
(3)求證：
<e4(n∈N*)．．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
(2)見解析
.
時,求函數
的單調區間;
,且
,求證:
;
,對于任意
時,總存在
,使
成立,求實數
的取值范圍.