已知O、A、M、B為平面上四點(diǎn),且
=λ+(1-λ),λ∈(-1,0),則( )
分析:化簡等式可得
=λ•
,可得
和
共線,再由λ∈(-1,0),得點(diǎn)A在線段BM上.
解答:解:由于
=λ+(1-λ),λ∈(-1,0),
∴
-=λ•(
-),即
=λ•
.
故
和
共線,且點(diǎn)A在線段BM上.
故選:C.
點(diǎn)評:本題考查平面向量基本定理及其幾何意義,得到
=λ•
,是解題的關(guān)鍵.
練習(xí)冊系列答案
相關(guān)習(xí)題
科目:高中數(shù)學(xué)
來源:
題型:
已知O、A、M、B為平面上四點(diǎn),且
=λ+(1-λ),λ∈(1,2),則( )
| A、點(diǎn)M在線段AB上 |
| B、點(diǎn)B在線段AM上 |
| C、點(diǎn)A在線段BM上 |
| D、O、A、M、B四點(diǎn)一定共線 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:不詳
題型:單選題
已知O、A、M、B為平面上四點(diǎn),且
=λ+(1-λ),λ∈(1,2),則( )
| A.點(diǎn)M在線段AB上 | B.點(diǎn)B在線段AM上 |
| C.點(diǎn)A在線段BM上 | D.O、A、M、B四點(diǎn)一定共線 |
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:2010-2011學(xué)年安徽省馬鞍山市當(dāng)涂二中高一第四次段考數(shù)學(xué)試卷(解析版)
題型:選擇題
已知O、A、M、B為平面上四點(diǎn),且
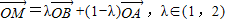
,則( )
A.點(diǎn)M在線段AB上
B.點(diǎn)B在線段AM上
C.點(diǎn)A在線段BM上
D.O、A、M、B四點(diǎn)一定共線
查看答案和解析>>
科目:高中數(shù)學(xué)
來源:2009-2010學(xué)年天津市武清區(qū)楊村四中高三(上)第三次月考數(shù)學(xué)試卷(理科)(解析版)
題型:選擇題
已知O、A、M、B為平面上四點(diǎn),且

,則( )
A.點(diǎn)M在線段AB上
B.點(diǎn)B在線段AM上
C.點(diǎn)A在線段BM上
D.O、A、M、B四點(diǎn)一定共線
查看答案和解析>>


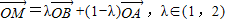 ,則( )
,則( ) ,則( )
,則( )