
是否存在常數(shù)a,b使等式 對于一切n∈N*都成立?若存在,求出a,b的值,若不存在,請說明理由。
對于一切n∈N*都成立?若存在,求出a,b的值,若不存在,請說明理由。
詳見解析.
【解析】
試題分析:先假設存在符合題意的常數(shù)a,b,c,再令n=1,n=2,n=3構造三個方程求出a,b,c,再用用數(shù)學歸納法證明成立,證明時先證:(1)當n=1時成立.(2)再假設n=k(k≥1)時,成立,遞推到n=k+1時,成立即可.
試題解析:【解析】
若存在常數(shù)a,b使得等式成立,將n=1,n=2代入等式
有:
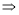
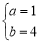
即有: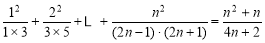 4分
4分
對于n為所有正整數(shù)是否成立,再用數(shù)學歸納法證明
證明:(1)當n=1時,等式成立。 5分
(2)假設n=k時等式成立,即
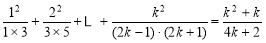 7分
7分
當n=k+1時,即
 11分
11分
也就是說n=k+1時,等式成立,
則: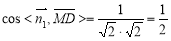
∴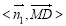 =60?
=60?
故:MD與平面OAC所成角為30? 8分
(3)設平面OBD的法向量為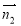 =(x,y,z),則
=(x,y,z),則

取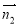 =(2,2,1)
=(2,2,1)
則點A到平面OBD的距離為d=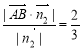 12分
12分
方法二:(1)由OA⊥底面ABCD,OA⊥BD。
∵底面ABCD是邊長為1的正方形
∴BD⊥AC ∴BD⊥平面OAC 4分
(2)設AC與BD交于點E,連結EM,則∠DME是直線MD與平面OAC折成的角
∵MD=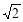 ,DE=
,DE=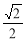
∴直線MD與平面OAC折成的角為30? 8分
(3)作AH⊥OE于點H。
∵BD⊥平面OAC
∴BO⊥AH
線段AH的長就是點A到平面OBD的距離。
∴AH=
∴點A到平面OBD的距離為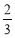 12分
12分
考點:1. 線面垂直的的判斷定理;2.線面成角.


科目:高中數(shù)學 來源:2015屆河南許昌市五高二上期期末聯(lián)考理科數(shù)學試卷(解析版) 題型:選擇題
若不等式 的解集是
的解集是 ,那么
,那么 的值是 ( )
的值是 ( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆河北邯鄲高二上學期期末考試理科數(shù)學試卷(解析版) 題型:選擇題
設雙曲線
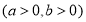 的虛軸長為2,焦距為
的虛軸長為2,焦距為 ,則雙曲線的漸近線方程為( )
,則雙曲線的漸近線方程為( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆河北邯鄲高二上學期期末考試文科數(shù)學試卷(解析版) 題型:選擇題
在等差數(shù)列 中,若
中,若 ,
, ,則公差
,則公差 等于( )
等于( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆江西贛州四所重點中學高二上學期期末聯(lián)考理數(shù)學試卷(解析版) 題型:填空題
雙曲線 的兩條漸近線將平面劃分為“上、下、左、右”四個區(qū)域(不含邊界),若點(1,2)在“上”區(qū)域內,則雙曲線離心率的取值范圍為 。
的兩條漸近線將平面劃分為“上、下、左、右”四個區(qū)域(不含邊界),若點(1,2)在“上”區(qū)域內,則雙曲線離心率的取值范圍為 。
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆江西贛州四所重點中學高二上學期期末聯(lián)考理數(shù)學試卷(解析版) 題型:選擇題
已知某幾何體的三視圖如圖所示,其中俯視圖中圓的直徑為4,該幾何體的體積為V1,直徑為4的球的體積為V2,則V1:V2等于( )

A.1:2
B.2:1
C.1:1
D.1:4
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆江西贛州四所重點中學高二上學期期末聯(lián)考文數(shù)學試卷(解析版) 題型:選擇題
設定點M1(0,-3),M2(0,3),動點P滿足條件|PM1|+|PM2|=a+ (其中a是正常數(shù)),則點P的軌跡是( )
(其中a是正常數(shù)),則點P的軌跡是( )
A.橢圓 B.線段
C.橢圓或線段 D.不存在
查看答案和解析>>
科目:高中數(shù)學 來源:2015屆江西贛州六校高二上學期期末聯(lián)考文科數(shù)學試卷(解析版) 題型:選擇題
設函數(shù)f(x)=xex,則( )
A.x=1為f(x)的極大值點 B.x=1為f(x)的極小值點
C.x=-1為f(x)的極大值點 D.x=-1為f(x)的極小值點
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com