
已知拋物線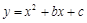 在點
在點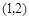 處的切線與直線
處的切線與直線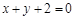 垂直,求函數
垂直,求函數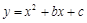 的最值.
的最值.
科目:高中數學 來源:2012年普通高等學校招生全國統一考試全國卷數學文科 題型:044
已知拋物線C:y=(x+1)2與圓M:(x-1)2+(y-![]() )2=r2(r>0)有一個公共點A,且在A處兩曲線的切線為同一直線上.
)2=r2(r>0)有一個公共點A,且在A處兩曲線的切線為同一直線上.
(Ⅰ)求r;
(Ⅱ)設m,n是異于l且與C及M都切的兩條直線,m,n的交點為D,求D到l的距離.
查看答案和解析>>
科目:高中數學 來源:高考真題 題型:解答題
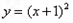 與圓
與圓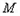 :
: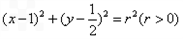 有一個公共點
有一個公共點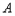 ,且在
,且在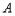 處兩曲線的切線為同一直線上。
處兩曲線的切線為同一直線上。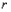 ;
;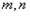 是異于
是異于 且與
且與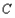 及
及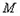 都切的兩條直線,
都切的兩條直線,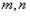 的交點為
的交點為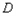 ,求
,求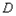 到
到 的距離。
的距離。查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com