
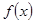 的定義域為
的定義域為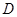 ,若存在閉區間
,若存在閉區間 ,使得函數
,使得函數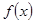 滿足以下兩個條件:(1)
滿足以下兩個條件:(1)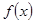 在[m,n]上是單調函數;(2)
在[m,n]上是單調函數;(2) 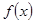 在[m,n]上的值域為[2m,2n],則稱區間[m,n]為
在[m,n]上的值域為[2m,2n],則稱區間[m,n]為 的“倍值區間”.下列函數中存在“倍值區間”的有 (填上所有正確的序號)
的“倍值區間”.下列函數中存在“倍值區間”的有 (填上所有正確的序號)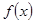 =x2(x≥0); ②
=x2(x≥0); ②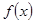 =ex(x∈R);
=ex(x∈R);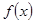 =
=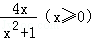 ;④
;④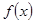 =
=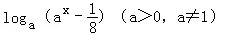 .
.湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com