
(滿分14分)設![]() ,在平面直角坐標系中,已知向量
,在平面直角坐標系中,已知向量![]() ,向
,向![]() 量
量![]() ,
,![]() ,動點
,動點![]() 的軌跡為E.
的軌跡為E.
(1)求軌跡E的方程,并說![]() 明該方程所表示曲線的形狀;
明該方程所表示曲線的形狀;
(2)已知![]() ,證明:存在圓心在原點的圓,使得該圓的任意一條切線與軌跡E恒有兩個交點A,B,且
,證明:存在圓心在原點的圓,使得該圓的任意一條切線與軌跡E恒有兩個交點A,B,且![]() (O為坐標
(O為坐標![]() 原點),并求出該圓的方程;
原點),并求出該圓的方程;
(3)已知![]() ,設直線
,設直線![]() 與圓C:
與圓C:![]() (1<R<2)相切于A1,且
(1<R<2)相切于A1,且![]() 與軌跡E只有一個公共點B1,當R為何值時,|A1B1|取得最大值?并求最大值.
與軌跡E只有一個公共點B1,當R為何值時,|A1B1|取得最大值?并求最大值.
(1)略 (2)![]() (3)
(3)![]()
(1)因為![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,即
,即![]() .當m=0時,方程表示兩直線,方程為
.當m=0時,方程表示兩直線,方程為![]() ;[來源:Z]當
;[來源:Z]當![]() 時, 方程表示的是圓;當
時, 方程表示的是圓;當![]() 且
且![]() 時,方程表示的是橢圓;當
時,方程表示的是橢圓;當![]() 時,方程表示的是雙曲線.
時,方程表示的是雙曲線.
(2)當![]() 時, 軌跡E的方程為
時, 軌跡E的方程為![]() ,設圓心在原點的圓的一條切線為
,設圓心在原點的圓的一條切線為![]() ,解方程組
,解方程組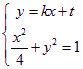 得
得![]() ,即
,即![]() ,
,
要使切線與軌跡E恒有兩個交點A,B,
則使△=![]() ,
,
即![]() ,即
,即![]() , 且
, 且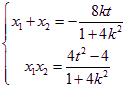
![]() ,
,
要使![]() , 需使
, 需使![]() ,即
,即![]() ,
,
所以![]() , 即
, 即![]() 且
且![]() , 即
, 即![]() 恒成立.
恒成立.
所以又因為直線![]() 為
為![]() 圓心在原點的圓的一條切線,所以圓的半徑為
圓心在原點的圓的一條切線,所以圓的半徑為![]() ,
,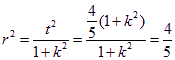 , 所求的圓為
, 所求的圓為![]() .
.
當切線的斜率不存在時,切線為![]() ,與
,與![]()
交于點![]() 或
或![]() 也滿足
也滿足![]() .
.
綜上, 存在圓心在原點的圓![]() ,
,
使得該圓的任意一條切線與橢圓E恒有兩個交點A,B,且![]() .
.
(3)當![]() 時,軌跡E的方程為
時,軌跡E的方程為![]() ,
,
設直線![]() 的方程為
的方程為![]() ,因為直線
,因為直線![]() 與圓C:
與圓C:![]() (1<R<2)相切于A1,
(1<R<2)相切于A1,
由(2)知![]() , 即
, 即![]() ①,
①,
因為![]() 與軌跡E只有一個公共點B1,由(2)知
與軌跡E只有一個公共點B1,由(2)知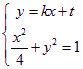 得
得![]()
![]() ,[來源:學科網]
,[來源:學科網]
即![]() 有唯一解,
有唯一解,
則△=![]() ,
,
即![]() , ②
, ②
由①②得 , 此時A,B重合為B1(x1,y1)點,
, 此時A,B重合為B1(x1,y1)點,
由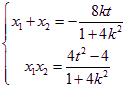 中
中![]() ,所以,
,所以,![]() ,
,
B1(x1,y1)點在橢圓上,所以![]() ,所以
,所以![]() ,
,
在直角三角形OA1B1中,![]()
因為![]() 當且僅當
當且僅當![]() 時取等號,所以
時取等號,所以![]() ,
,
即當![]() 時|A1B1|取得最大值,最大值為1.
時|A1B1|取得最大值,最大值為1.


 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:高中數學 來源:2012-2013學年廣東省云浮市高三第五次月考文科數學試卷(解析版) 題型:解答題
(本小題滿分14分)設定義在(0,+ )上的函數
)上的函數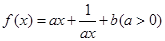
(Ⅰ)求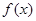 的最小值;
的最小值;
(II)若曲線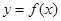 在點
在點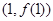 處的切線方程為
處的切線方程為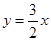 ,求
,求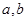 的值.
的值.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年福建省四地六校聯考高三上學期第二次月考文科數學卷 題型:解答題
(本小題滿分14分)
設函數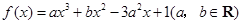 在
在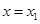 ,
,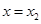 處取得極值,且
處取得極值,且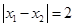 .
.
(Ⅰ)若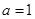 ,求
,求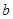 的值,并求
的值,并求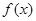 的單調區(qū)間;
的單調區(qū)間;
(Ⅱ)若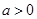 ,求
,求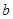 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省中山市高三第三次月考數學文卷 題型:解答題
(本小題滿分14分)
設函數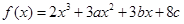 在
在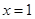 及
及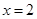 時取得極值.
時取得極值.
(1)求a、b的值;
(2)若對于任意的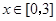 ,都有
,都有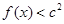 成立,求c的取值范圍.
成立,求c的取值范圍.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com