
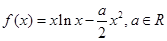
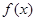 在(0,
在(0,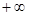 )單調遞減,求a的最小值
)單調遞減,求a的最小值 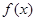 有兩個極值點,求a的取值范圍.
有兩個極值點,求a的取值范圍.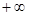 )單調遞減”轉化為“"x∈(0,+∞),a≥
)單調遞減”轉化為“"x∈(0,+∞),a≥ ”,然后才有構造函數的思想求解函數的最大值即可;(Ⅱ)通過對參數a 與1的討論,借助求導的方法研究函數的單調性,進而分析保證有兩個極值點的條件,通過解不等式求解求a的取值范圍.
”,然后才有構造函數的思想求解函數的最大值即可;(Ⅱ)通過對參數a 與1的討論,借助求導的方法研究函數的單調性,進而分析保證有兩個極值點的條件,通過解不等式求解求a的取值范圍. . ①
. ① ,則g¢(x)=-
,則g¢(x)=- .
.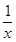 -a.
-a. )時,h¢(x)>0,h(x)單調遞增;
)時,h¢(x)>0,h(x)單調遞增; ,+∞)時,h¢(x)<0,h(x)單調遞減. 9分
,+∞)時,h¢(x)<0,h(x)單調遞減. 9分 )=h(
)=h( )=ln
)=ln >0,f¢(
>0,f¢( )=h(
)=h( )=-
)=- <0,
<0, ,
, )有一極小值點x1. 10分
)有一極小值點x1. 10分 ,即lnx≤x-1,則ln
,即lnx≤x-1,則ln ≤
≤ -1,
-1, )=h(
)=h( )=ln2+2ln
)=ln2+2ln +1-
+1- ≤ln2+2(
≤ln2+2( -1)+1-
-1)+1- =ln2-1<0.
=ln2-1<0. ,
, )有一極大值點x2.
)有一極大值點x2.

 孟建平小學滾動測試系列答案
孟建平小學滾動測試系列答案 黃岡天天練口算題卡系列答案
黃岡天天練口算題卡系列答案科目:高中數學 來源:不詳 題型:解答題
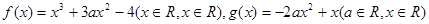 (Ⅰ)若函數
(Ⅰ)若函數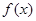 在
在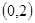 上單調遞減,在區間
上單調遞減,在區間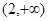 單調遞增,求
單調遞增,求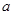 的值;
的值;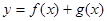 在
在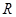 上有兩個不同的極值點,求
上有兩個不同的極值點,求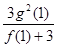 的取值范圍;
的取值范圍;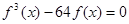 有且只有三個不同的實根,求
有且只有三個不同的實根,求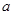 的取值范圍。
的取值范圍。查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
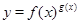 的函數的導數,我們常采用以下做法:先兩邊同取自然對數得:
的函數的導數,我們常采用以下做法:先兩邊同取自然對數得: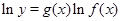 ,再兩邊同時求導得
,再兩邊同時求導得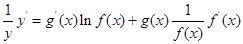 ,于是得到:
,于是得到: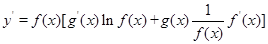 ,運用此方法求得函數
,運用此方法求得函數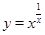 的一個單調遞增區間是( )
的一個單調遞增區間是( )A. | B. | C. | D. |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com