
設{an}是公比為正數的等比數列,a1=2,a3=a2+4.
(1)求{an}的通項公式.
(2)設{bn}是首項為1,公差為2的等差數列,求{an+bn}的前n項和Sn.
 學練快車道快樂假期暑假作業新疆人民出版社系列答案
學練快車道快樂假期暑假作業新疆人民出版社系列答案 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:高中數學 來源: 題型:解答題
已知數列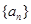 的各項均為正數,記
的各項均為正數,記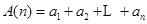 ,
,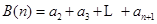 ,
,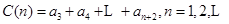 .
.
(1)若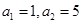 ,且對任意
,且對任意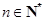 ,三個數
,三個數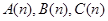 組成等差數列,求數列
組成等差數列,求數列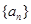 的通項公式.
的通項公式.
(2)證明:數列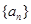 是公比為
是公比為 的等比數列的充分必要條件是:對任意
的等比數列的充分必要條件是:對任意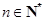 ,三個數
,三個數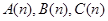 組成公比為
組成公比為 的等比數列.
的等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在無窮數列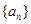 中,
中,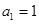 ,對于任意
,對于任意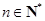 ,都有
,都有 ,
,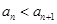 . 設
. 設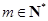 , 記使得
, 記使得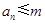 成立的
成立的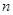 的最大值為
的最大值為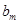 .
.
(1)設數列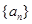 為1,3,5,7,
為1,3,5,7,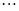 ,寫出
,寫出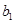 ,
,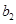 ,
,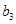 的值;
的值;
(2)若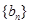 為等差數列,求出所有可能的數列
為等差數列,求出所有可能的數列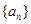 ;
;
(3)設 ,
,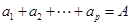 ,求
,求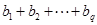 的值.(用
的值.(用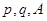 表示)
表示)
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知數列{an}中,a1=2,an=2-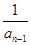 (n≥2,n∈N*).
(n≥2,n∈N*).
(1)設bn=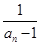 ,n∈N*,求證:數列{bn}是等差數列;
,n∈N*,求證:數列{bn}是等差數列;
(2)設cn=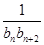 (n∈N*),求數列{cn}的前n項和Sn.
(n∈N*),求數列{cn}的前n項和Sn.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
數列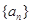 的前n項和為
的前n項和為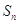 ,存在常數A,B,C,使得
,存在常數A,B,C,使得 對任意正整數n都成立.
對任意正整數n都成立.
⑴若數列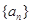 為等差數列,求證:3A B+C=0;
為等差數列,求證:3A B+C=0;
⑵若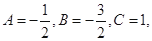 設
設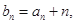 數列
數列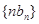 的前n項和為
的前n項和為 ,求
,求 ;
;
⑶若C=0,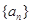 是首項為1的等差數列,設
是首項為1的等差數列,設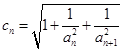 數列
數列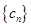 的前2014項和為P,求不超過P的最大整數的值.
的前2014項和為P,求不超過P的最大整數的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com