

(2)若P是棱長均為a的正四面體S—ABC內任意一點,試證明點P到各側面的距離之和為定值.
思路解析:(1)連結PA、PB、PC,將正三角形分割成三個小三角形,利用三角形面積不變即可求得點P到各邊的距離之和為定值.
(2)運用“類比”法進行求解.平面→空間:正三角形→正四面體;面積→體積;分割→分割;內分小三角形→內分小四面體;小三角形一邊長→四面體底面積.于是可將正四面體S—ABC分割成四個以點P為頂點,四個面為底面的小三棱錐.利用正四面體的體積不變求得點P到各側面的距離之和為定值.
(1)證明:設P到各邊的距離分別為m、l、n,則有△ABC的面積等于三個小三角形△APC、△APB、△BPC的面積的和,列式即為
S△ABC=S△APC+S△APB+S△BPC=![]() al+
al+![]() am+
am+![]() an=
an=![]() a(l+m+n)=
a(l+m+n)=![]() a2,
a2,
得到l+m+n=![]() a.
a.

(2)解:設P到四面體各面的距離分別為m、l、n、h,則四面體SABC的體積等于四個小四面體P—ABC、P—SBC、P—SAC、P—SAB的體積之和,列式計算即為
VS—ABC=VP—ABC+VP—SBC+VP—SAC+VP—SAB=![]() ·
·![]() a2·(l+m+n+h)=
a2·(l+m+n+h)=![]() a3.
a3.
得到l+m+n+h=a.
方法歸納 用等積法求點到平面的距離的步驟:
(1)設距離為h,把h看成某三棱錐的高;
(2)把三棱錐的另一面看成底面,求出體積;
(3)由體積相等求出相應的距離.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
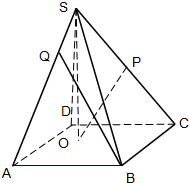 如圖,已知四棱錐S-ABCD的底面是邊長為4的正方形,S在底面上的射影O落在正方形ABCD內,SO的長為3,O到AB,AD的距離分別為2和1,P是SC的中點.
如圖,已知四棱錐S-ABCD的底面是邊長為4的正方形,S在底面上的射影O落在正方形ABCD內,SO的長為3,O到AB,AD的距離分別為2和1,P是SC的中點.| AQ |
| 3 |
| 4 |
| AS |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2013•日照一模)如圖,四邊形ABCD是正方形,延長CD至E,使得DE=CD.若動點P從點A出發,沿正方形的邊按逆時針方向運動一周回到A點,其中
(2013•日照一模)如圖,四邊形ABCD是正方形,延長CD至E,使得DE=CD.若動點P從點A出發,沿正方形的邊按逆時針方向運動一周回到A點,其中| AP |
| AB |
| AE |
查看答案和解析>>
科目:高中數學 來源:2007年普通高等學校招生全國統一考試、文科數學(上海卷) 題型:044
我們把由半橢圓![]() (x≥0)與半橢圓
(x≥0)與半橢圓![]() (x≤0)合成的曲線稱作“果圓”,其中a2=b2+c2,a>0,b>c>0.
(x≤0)合成的曲線稱作“果圓”,其中a2=b2+c2,a>0,b>c>0.
如圖,設點F0,F1,F2是相應橢圓的焦點,A1,A2和B1,B2是“果圓”與x,y軸的交點,M是線段A1A2的中點.

(1)若△F0F1F2是邊長為1的等邊三角形,求該“果圓”的方程;
(2)設P是“果圓”的半橢圓![]() (x≤0)上任意一點.求證:當|PM|取得最小值時,P在點B1,B2或A1處;
(x≤0)上任意一點.求證:當|PM|取得最小值時,P在點B1,B2或A1處;
(3)若P是“果圓”上任意一點,求|PM|取得最小值時點P的橫坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com