
如圖,三棱柱ABC-A1B1C1的側(cè)棱AA1⊥平面ABC,△ABC為正三角形,且側(cè)面AA1C1C是邊長(zhǎng)為2的正方形,E是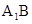 的中點(diǎn),F在棱CC1上。
的中點(diǎn),F在棱CC1上。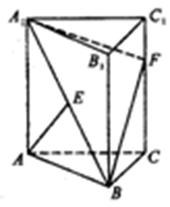
(1)當(dāng)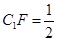 CF時(shí),求多面體ABCFA1的體積;
CF時(shí),求多面體ABCFA1的體積;
(2)當(dāng)點(diǎn)F使得A1F+BF最小時(shí),判斷直線AE與A1F是否垂直,并證明的結(jié)論。
(1) 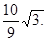 ;(2)
;(2) 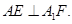 ,證明詳見解析
,證明詳見解析
解析試題分析:(1)此多面體是以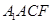 為底面,以B為頂點(diǎn)的四棱錐,而且
為底面,以B為頂點(diǎn)的四棱錐,而且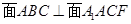 ,因?yàn)椤鰽BC為正三角形,所以△ABC的AC邊上的高即為此四棱錐的高,底面
,因?yàn)椤鰽BC為正三角形,所以△ABC的AC邊上的高即為此四棱錐的高,底面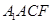 是直角梯形,所以利用錐體體積公式即可求得其體積。(2)把立體圖展成平面圖后,兩點(diǎn)之間直線最短,連接
是直角梯形,所以利用錐體體積公式即可求得其體積。(2)把立體圖展成平面圖后,兩點(diǎn)之間直線最短,連接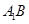 交
交 與點(diǎn)F,此時(shí)A1F+BF最小,分析可知F為
與點(diǎn)F,此時(shí)A1F+BF最小,分析可知F為 的中點(diǎn)。過點(diǎn)
的中點(diǎn)。過點(diǎn) 作
作 交
交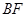 于
于 ,則
,則 是
是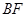 的中點(diǎn),此時(shí)只需判斷AE與EG是否垂直即可。求出三角形AEG三邊長(zhǎng)即可得證,詳見解析。
的中點(diǎn),此時(shí)只需判斷AE與EG是否垂直即可。求出三角形AEG三邊長(zhǎng)即可得證,詳見解析。
試題解析:解:(Ⅰ)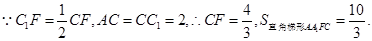
由已知可得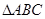 的高為
的高為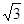 且等于四棱錐
且等于四棱錐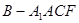 的高.
的高.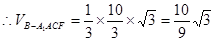 ,即多面體
,即多面體 的體積為
的體積為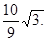 5分
5分
(Ⅱ)將側(cè)面 展開到側(cè)面
展開到側(cè)面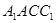 得到矩形
得到矩形 ,連結(jié)
,連結(jié) ,交
,交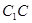 于點(diǎn)
于點(diǎn) ,此時(shí)點(diǎn)
,此時(shí)點(diǎn) 使得
使得 最小.此時(shí)
最小.此時(shí) 平行且等于
平行且等于 的一半,
的一半,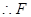 為
為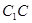 的中點(diǎn). 7分
的中點(diǎn). 7分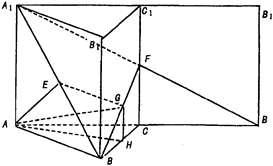
過點(diǎn) 作
作 交
交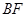 于
于 ,則
,則 是
是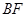 的中點(diǎn),
的中點(diǎn),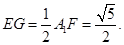 .
.
過點(diǎn) 作
作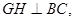 交
交 于
于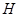 ,則
,則
又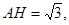 于是在
于是在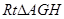 中,
中, 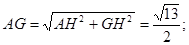
在 中,
中,
在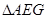 中,
中,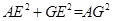 ,
, ∴
∴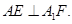 13分
13分
考點(diǎn):幾何體體積,線線垂直。


 黎明文化寒假作業(yè)系列答案
黎明文化寒假作業(yè)系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖所示是一幾何體的直觀圖、正(主)視圖、側(cè)(左)視圖、俯視圖.
(1)若F為PD的中點(diǎn),求證:AF⊥面PCD;
(2)求幾何體BEC-APD的體積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖在長(zhǎng)方體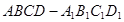 中,
中,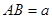 ,
,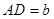 ,
,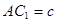 ,點(diǎn)
,點(diǎn)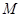 為
為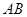 的中點(diǎn),點(diǎn)
的中點(diǎn),點(diǎn)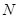 為
為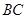 的中點(diǎn).
的中點(diǎn).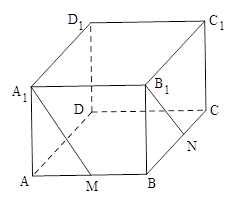
(1)求長(zhǎng)方體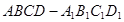 的體積;
的體積;
(2)若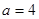 ,
,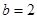 ,
,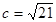 ,求異面直線
,求異面直線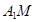 與
與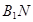 所成的角.
所成的角.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知半徑為 的球內(nèi)有一個(gè)內(nèi)接正方體(即正方體的頂點(diǎn)都在球面上).
的球內(nèi)有一個(gè)內(nèi)接正方體(即正方體的頂點(diǎn)都在球面上).
(1)求此球的體積;
(2)求此球的內(nèi)接正方體的體積;
(3)求此球的表面積與其內(nèi)接正方體的全面積之比.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知幾何體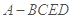 的三視圖如圖所示,其中俯視圖和側(cè)視圖都是腰長(zhǎng)為4的等腰直角三角形,正視圖為直角梯形.
的三視圖如圖所示,其中俯視圖和側(cè)視圖都是腰長(zhǎng)為4的等腰直角三角形,正視圖為直角梯形.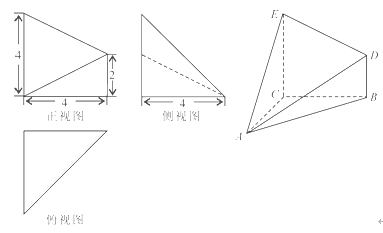
(1)求異面直線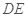 與
與 所成角的余弦值;
所成角的余弦值;
(2)求二面角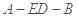 的正弦值;
的正弦值;
(3)求此幾何體的體積的大小
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
如圖,在四棱錐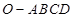 中,底面
中,底面 是邊長(zhǎng)為
是邊長(zhǎng)為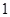 的菱形,
的菱形,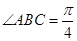 ,
, 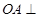 底面
底面 ,
,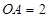 ,
,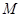 為
為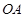 的中點(diǎn),
的中點(diǎn),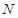 為
為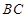 的中點(diǎn).
的中點(diǎn).
(Ⅰ)求四棱錐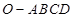 的體積;
的體積;
(Ⅱ)證明:直線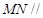 平面
平面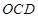 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:解答題
已知四棱錐 的底面為直角梯形,
的底面為直角梯形,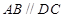 ,
,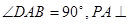 底面
底面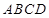 ,且
,且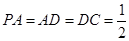 ,
,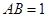 ,
,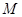 是
是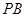 的中點(diǎn)。
的中點(diǎn)。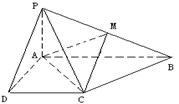
(Ⅰ)證明:面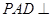 面
面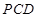 ;
;
(Ⅱ)求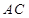 與
與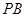 所成的角;
所成的角;
(Ⅲ)求面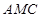 與面
與面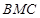 所成二面角的大小。
所成二面角的大小。
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com