
已知函數 (
( ).
).
(1)當 時,求函數
時,求函數 的單調區間;
的單調區間;
(2)當 時,
時, 取得極值.
取得極值.
① 若 ,求函數
,求函數 在
在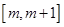 上的最小值;
上的最小值;
② 求證:對任意 ,都有
,都有 .
.
(1)單調增區間為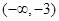 和
和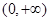 ,單調減區間為
,單調減區間為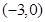 ;(2)①
;(2)①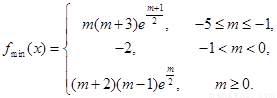 ②詳見解析.
②詳見解析.
【解析】
試題分析:(1)求導解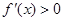 得
得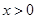 或
或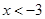 ,
解
,
解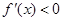 得
得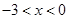 ;
;
(2)①當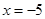 時,
時,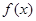 取得極值, 所以
取得極值, 所以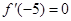 解得
解得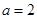 ,對
,對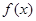 求導,判斷在
求導,判斷在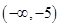 ,
,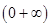 遞增,在
遞增,在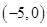 遞減,分類討論,求出最小值;②通過求導,求出
遞減,分類討論,求出最小值;②通過求導,求出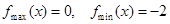 ,將恒成立問題轉化為最值問題,對任意
,將恒成立問題轉化為最值問題,對任意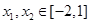 ,都有
,都有 .
.
試題解析:(1)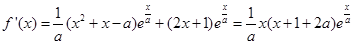
當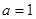 時,
時,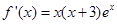
解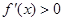 得
得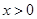 或
或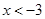 ,
解
,
解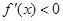 得
得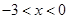
所以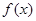 單調增區間為
單調增區間為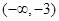 和
和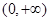 ,單調減區間為
,單調減區間為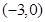
(2)①當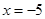 時,
時,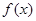 取得極值, 所以
取得極值, 所以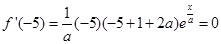
解得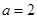 (經檢驗
(經檢驗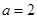 符合題意)
符合題意)
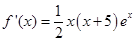
|
|
|
|
|
|
|
|
|
+ |
0 |
- |
0 |
+ |
|
|
|
|
↘ |
|
↗ |
所以函數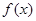 在
在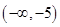 ,
,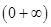 遞增,在
遞增,在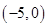 遞減
遞減
當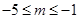 時,
時,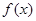 在
在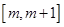 單調遞減,
單調遞減,
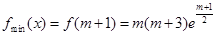
當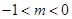 時
時 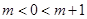
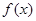 在
在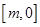 單調遞減,在
單調遞減,在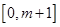 單調遞增,
單調遞增,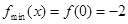
當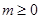 時,
時,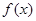 在
在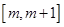 單調遞增,
單調遞增,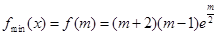
綜上,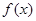 在
在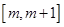 上的最小值
上的最小值
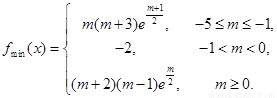
②令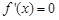 得
得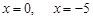 (舍)
(舍)
因為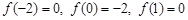 所以
所以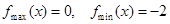
所以,對任意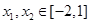 ,都有
,都有 .
.
考點:求導,函數單調性,函數最值,恒成立問題.


科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3 |
| π |
| 24 |
| 5π |
| 24 |
| π |
| 24 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 11π |
| 6 |
| ||
| 2 |
| 3 |
| π |
查看答案和解析>>
科目:高中數學 來源: 題型:
| xn+2 | xn-2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函數f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<| π |
| 2 |
A、f(x)=2sin(
| ||||
B、f(x)=2sin(
| ||||
C、f(x)=2sin(2x-
| ||||
D、f(x)=2sin(2x+
|
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com