
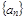 中,
中,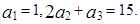
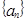 通項公式;
通項公式;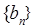 滿足
滿足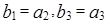 ,求數列
,求數列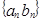 的前
的前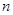 項和
項和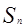 。
。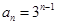 ;(Ⅱ)
;(Ⅱ)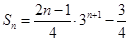 .
.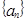 通項公式,由題意,
通項公式,由題意,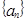 是各項均為正數的等比數列,故求出
是各項均為正數的等比數列,故求出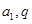 即可,根據
即可,根據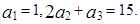 ,利用等比數列的通項公式,求出公比,從而可得數列
,利用等比數列的通項公式,求出公比,從而可得數列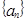 的通項公式;(Ⅱ)求數列
的通項公式;(Ⅱ)求數列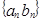 的前項
的前項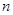 和
和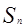 ,首先確定數列
,首先確定數列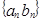 的通項公式,即先確定等差數列
的通項公式,即先確定等差數列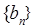 的通項公式,由(Ⅰ)知,
的通項公式,由(Ⅰ)知,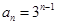 ,利用
,利用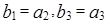 ,可求得,
,可求得,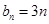 ,從而可得,
,從而可得,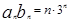 ,這是一個等差數列與一個等比數列對應項積所組成的數列,故可利用利用錯位相減法,可求數列
,這是一個等差數列與一個等比數列對應項積所組成的數列,故可利用利用錯位相減法,可求數列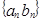 的前
的前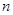 項和
項和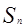 .
.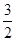 (3n-1)-n×3n+1 (11分)
(3n-1)-n×3n+1 (11分) 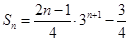 (12分)
(12分)

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com