


 ,設
,設
(Ⅰ)求函數 的周期及單調增區間。
的周期及單調增區間。
(Ⅱ)設 的內角
的內角 的對邊分別為
的對邊分別為 ,已知
,已知
 ,求邊
,求邊 的值.
的值.
單調遞增區間是[2k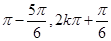 ],周期T=2
],周期T=2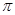 ;(Ⅱ)
;(Ⅱ)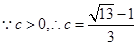
【解析】此題考查了正弦、余弦定理,三角函數的周期性及其求法,以及三角函數的恒等變換應用,涉及的知識有:兩角和與差的正弦函數公式,二倍角的余弦函數公式,正弦函數的單調性,同角三角函數間的基本關系,以及三角形的邊角關系,熟練掌握定理及公式是解本題的關鍵。
(1)(1)由兩向量的坐標,利用平面向量的數量積運算法則列出關系式,再利用兩角和與差的直正弦函數公式及二倍角的余弦函數公式化簡,整理后得到一個角的正弦函數,找出ω的值,代入周期公式,即可求出函數的最小正周期;根據正弦函數的單調遞減區間列出關于x的不等式,求出不等式的解集即可得到函數的遞減區間;
(2)由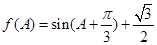
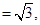 ,
,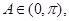 得
得 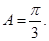
由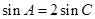 得
得 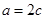 .又
.又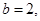 結合余弦定理得到結論。
結合余弦定理得到結論。
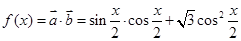
=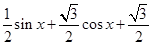
=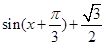

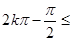 x+
x+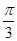
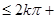
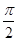 ……即2k
……即2k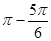
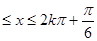 ……
……
所以…函數的單調遞增區間是[2k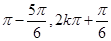 ],
],
周期T=2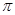 6分
6分
(Ⅱ)由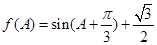
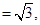 ,
,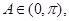 得
得 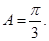
由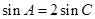 得
得 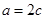 .又
.又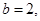
由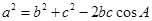 得
得 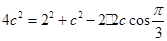
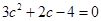 ,
,
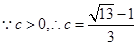 …………………………12分
…………………………12分


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
| 1 | 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 5 | 3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com