
��D����֪�E�A �ķ��̞�
�ķ��̞� ���p����
���p���� �ăɗl�u������
�ăɗl�u������ ��
�� .�^(gu��)�E�A
.�^(gu��)�E�A ���ҽ��c(di��n)
���ҽ��c(di��n) ��ֱ��
��ֱ�� ��ʹ
��ʹ ����
���� �c
�c �����c(di��n)
�����c(di��n) ���O(sh��)
���O(sh��) �c�E�A
�c�E�A �ăɂ�(g��)���c(di��n)�����������Ξ�
�ăɂ�(g��)���c(di��n)�����������Ξ� ��
�� .
.

��1���� �c
�c �ĊA�Ǟ�
�ĊA�Ǟ� �����p�����Ľ�����
�����p�����Ľ����� ����E�A
����E�A �ķ��̣�
�ķ��̣�
��2���� �����ֵ.
�����ֵ.
��1��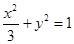 ����2��
����2�� .
.
��������
ԇ�}��������1���ȴ_���p�����ĝu�������̣�����(j��)�l���ɗl�u�����ĊA�Ǟ� ���_��
���_�� �c
�c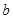 �ĵ����P(gu��n)ϵ���ٽY(ji��)��
�ĵ����P(gu��n)ϵ���ٽY(ji��)�� ��ֵ���_��
��ֵ���_�� �c
�c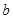 ��ֵ����K�_���E�A
��ֵ����K�_���E�A �ķ��̣���2���O(sh��)�c(di��n)
�ķ��̣���2���O(sh��)�c(di��n) ������(bi��o)��
������(bi��o)��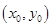 �����O(sh��)
�����O(sh��) �õ�
�õ� ����������������(bi��o)�\(y��n)��õ�
����������������(bi��o)�\(y��n)��õ� ��
�� �������c(di��n)
�������c(di��n) �ڙE�A
�ڙE�A ���@һ�l�����c(di��n)
���@һ�l�����c(di��n) ������(bi��o)����E�A���̣�ͨ�^(gu��)����(ji��n)�õ�
������(bi��o)����E�A���̣�ͨ�^(gu��)����(ji��n)�õ� �c�x����
�c�x���� ֮�g���P(gu��n)ϵʽ
֮�g���P(gu��n)ϵʽ ���Y(ji��)�ϻ�������ʽ�õ�
���Y(ji��)�ϻ�������ʽ�õ� �����ֵ.
�����ֵ.
ԇ�}��������1����?y��n)��p�������̞� ��
��
�����p�����ĝu�������̞� ��
��
��?y��n)�ɝu�����ĊA�Ǟ� ��
��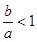 ������
������ ��
��
����
 ������
������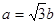 ��
��

��?y��n)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014032004575686094337/SYS201403200458470328544400_DA.files/image025.png">������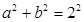 ��
��
���� ��
�� ��
��
���ԙE�A �ķ��̞�
�ķ��̞�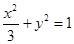 ��
��
��2����?y��n)?img src="http://thumb.zyjl.cn//pic6/res/gzsx/web/STSource/2014032004575686094337/SYS201403200458470328544400_DA.files/image029.png">������ֱ�� �c�ķ��̞�
�c�ķ��̞� ������
������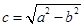 .
.
��?y��n)�ֱ�� �ķ��̞�
�ķ��̞�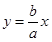 ��
��
(li��n)��ֱ�� �c
�c �ķ��̽���c(di��n)
�ķ��̽���c(di��n) .
.
�O(sh��) ���t
���t .
.
��?y��n)��c(di��n)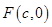 ���O(sh��)�c(di��n)
���O(sh��)�c(di��n) ���t��
���t�� ��
��
��� ��
�� .
.
��?y��n)��c(di��n) �ڙE�A
�ڙE�A �ϣ�
�ϣ�
����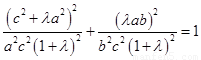 ��
��
��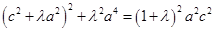 ��
��
��ʽ��߅ͬ���� ��
�� ��
�� ��
��
���� ��
��
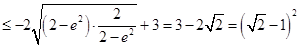
���Ԯ�(d��ng) ����
���� �r(sh��)��
�r(sh��)�� ȡ�����ֵ
ȡ�����ֵ ��
��
�� �����ֵ��
�����ֵ�� .
.
���c(di��n)��1.�p�����ĝu�������̣�2.�E�A�ķ��̣�3.���c(di��n)�������D(zhu��n)��


 ȫ��(y��u)�c(di��n)����ԪӋ(j��)��ϵ�д�
ȫ��(y��u)�c(di��n)����ԪӋ(j��)��ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
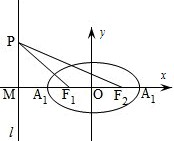 ��D����֪�E�A������������(bi��o)ԭ�c(di��n)�����c(di��n)F1��F(xi��n)2��x�S�ϣ��L(zh��ng)�SA1A2���L(zh��ng)��4�����(zh��n)��l�cx�S�Ľ��c(di��n)��M��|MA1|��|A1F1|=2��1��
��D����֪�E�A������������(bi��o)ԭ�c(di��n)�����c(di��n)F1��F(xi��n)2��x�S�ϣ��L(zh��ng)�SA1A2���L(zh��ng)��4�����(zh��n)��l�cx�S�Ľ��c(di��n)��M��|MA1|��|A1F1|=2��1���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
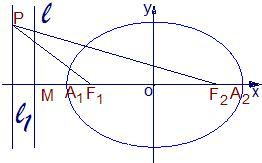 ��D����֪�E�A������������(bi��o)ԭ�c(di��n)�����c(di��n)F1��F(xi��n)2��x�S�ϣ��L(zh��ng)�SA1A2���L(zh��ng)��4�����(zh��n)��l�cx�S�Ľ��c(di��n)��M��|MA1|��|A1F1|=2��1��
��D����֪�E�A������������(bi��o)ԭ�c(di��n)�����c(di��n)F1��F(xi��n)2��x�S�ϣ��L(zh��ng)�SA1A2���L(zh��ng)��4�����(zh��n)��l�cx�S�Ľ��c(di��n)��M��|MA1|��|A1F1|=2��1���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
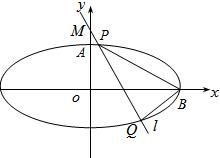 ��D����֪�E�A������������(bi��o)ԭ�c(di��n)�����c(di��n)��x�S�ϣ�����һ��(g��)��c(di��n)��A��0��
��D����֪�E�A������������(bi��o)ԭ�c(di��n)�����c(di��n)��x�S�ϣ�����һ��(g��)��c(di��n)��A��0��| 2 |
| ||
| 2 |
| PB |
| QB |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
��D����֪�E�A![]() �ķ��̞�
�ķ��̞�![]() ��
��![]() ����������c(di��n)��
����������c(di��n)��![]() ���ҽ��c(di��n)��
���ҽ��c(di��n)��![]() �����L(zh��ng)���c�E�A�����Ҝ�(zh��n)���քe�ཻ��
�����L(zh��ng)���c�E�A�����Ҝ�(zh��n)���քe�ཻ��![]() ���c(di��n)�����c(di��n)
���c(di��n)�����c(di��n)![]() ǡ�Þ�
ǡ�Þ�![]() ���c(di��n)���t�˙E�A���x���ʞ�_(k��i)_________
���c(di��n)���t�˙E�A���x���ʞ�_(k��i)_________

�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com