
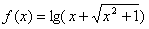 。
。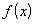 的奇偶性,并給予證明;
的奇偶性,并給予證明;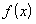 在其定義域上是單調增函數。
在其定義域上是單調增函數。  53隨堂測系列答案
53隨堂測系列答案科目:高中數學 來源:設計必修一數學(人教A版) 人教A版 題型:022
根據定義討論(或證明)函數增減性的一般步驟是:
(1)設x1、x2是給定區間內的任意兩個值且x1<x2;
(2)作差f(x1)-f(x2),并將此差化簡、變形;
(3)判斷f(x1)-f(x2)的正負,從而證得函數的增減性.
利用函數的單調性可以把函數值的大小比較的問題轉化為自變量的大小比較的問題.
函數的單調性只能在函數的定義域內來討論.這即是說,函數的單調區間是其定義域的________.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com