
(本小題12分)
設![]() ,對于有窮數列
,對于有窮數列![]() (
(![]() …,
…,![]() ), 令
), 令![]() 為
為![]() …,
…,![]() 中的最大值,稱數列
中的最大值,稱數列![]() 為
為![]() 的“創新數列”. 數列
的“創新數列”. 數列![]() 中不相等項的個數稱為
中不相等項的個數稱為![]() 的“創新階數”. 例如數列
的“創新階數”. 例如數列![]() 的創新數列為2,2,3,7,7,創新階數為3.
的創新數列為2,2,3,7,7,創新階數為3.
考察自然數![]() …,
…,![]()
![]() 的所有排列,將每種排列都視為一個有窮數列
的所有排列,將每種排列都視為一個有窮數列![]() .
.
(Ⅰ)若![]() , 寫出創新數列為3,4,4,5,5的所有數列
, 寫出創新數列為3,4,4,5,5的所有數列![]() ;
;
(Ⅱ) 是否存在數列![]() ,使它的創新數列為等差數列?若存在,求出所有的數列
,使它的創新數列為等差數列?若存在,求出所有的數列![]() ,若不存在,請說明理由.
,若不存在,請說明理由.
(Ⅰ)解:由題意,創新數列為3,4,4,5,5的數列![]() 有兩個,即:
有兩個,即:
(1)數列3,4,1,5,2; ……………………………… 3分
(2)數列3,4,2,5,1. ……………………… 5分
(Ⅱ)解:設數列![]() 的創新數列為
的創新數列為![]() ,
,
因為![]() 為
為![]() 中的最大值. 所以.
中的最大值. 所以.![]()
由題意知:![]() 為
為![]() 中最大值,
中最大值,![]() 為
為![]() 中最大值,
中最大值,
所以![]() ,且
,且![]() .
.
若![]() 為等差數列,設其公差為d,
為等差數列,設其公差為d,
則![]() ,且
,且![]() ……………………… …… 7分
……………………… …… 7分
當d=0時,![]() 為常數列,又
為常數列,又![]() ,所以數列
,所以數列![]() 為
為![]() ,
,
此時數列![]() 是首項為m的任意一個符合條件的數列;……… 8分
是首項為m的任意一個符合條件的數列;……… 8分
當d=1時,因為![]() ,所以數列
,所以數列![]() 為
為![]() ,
,
此時數列![]() 是
是![]() ; ……………………… 9分
; ……………………… 9分
當![]() 時,因為
時,因為![]() ,又
,又![]() ,所以
,所以![]() ,
,
這與![]() 矛盾,所以此時
矛盾,所以此時![]() 不存在,
不存在,
即不存在![]() 使得它的創新數列
使得它的創新數列
為![]() 的等差數列. ……………………… 11分
的等差數列. ……………………… 11分
綜上,當數列![]() 為首項為m的任意符合條件的數列或為數列
為首項為m的任意符合條件的數列或為數列![]() 時,
時,
它的創新數列為等差數列. …………………………


 新輔教導學系列答案
新輔教導學系列答案 陽光同學一線名師全優好卷系列答案
陽光同學一線名師全優好卷系列答案科目:高中數學 來源:2011年河南省衛輝市高二上學期末理科數學卷 題型:解答題
(本小題12分)
設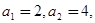 數列
數列 滿足:
滿足:
 ,
,
(1)求證:數列 是等比數列(要指出首項與公比),
是等比數列(要指出首項與公比),
(2)求數列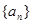 的通項公式
的通項公式
查看答案和解析>>
科目:高中數學 來源:2010年甘肅省高一下學期期末考試數學卷 題型:解答題
(本小題12分)設函數

(1)、求函數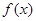 的最大值和最小正周期;
的最大值和最小正周期;
(2)、將函數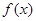 的圖像按向量
的圖像按向量 平移,使平移后得到的圖像關于坐標原點成中心對稱,求長度最小的向量
平移,使平移后得到的圖像關于坐標原點成中心對稱,求長度最小的向量 。
。
查看答案和解析>>
科目:高中數學 來源:2010-2011年新疆農七七師高級中學高二下學期第一學段考試理科數學 題型:解答題
(本小題12分)
設函數 。
。
(1)若曲線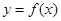 在點
在點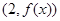 處與直線
處與直線 相切,求
相切,求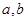 的值;
的值;
(2)求函數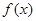 的單調區間與極值點。
的單調區間與極值點。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com