
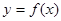 ,對任意不等的實數
,對任意不等的實數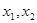 都有
都有 成立,又函數
成立,又函數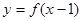 的圖象關于點(1,0)對稱,若不等式
的圖象關于點(1,0)對稱,若不等式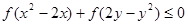 成立,則當1≤x<4時,
成立,則當1≤x<4時,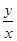 的取值范圍是
的取值范圍是A.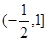 | B.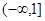 | C.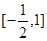 | D.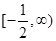 |
 所以函數f(x)是定義在R上的單調遞減函數.因為函數y=f(x-1)的圖象關于點(1,0)對稱,所以函數y=f(x)的圖象關于點(0,0)對稱,即函數f(x)是定義在R上的奇函數.又因為對于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立,所以f(x2-2x)≥f(-2y+y2)成立,所以根據函數的單調性可得:對于任意的x,y∈R,不等式x2-2x≥y2-2y成立,即(x-y)(x+y-2)≥0(1≤x≤4),所以可得其可行域,如圖所示:
所以函數f(x)是定義在R上的單調遞減函數.因為函數y=f(x-1)的圖象關于點(1,0)對稱,所以函數y=f(x)的圖象關于點(0,0)對稱,即函數f(x)是定義在R上的奇函數.又因為對于任意的x,y∈R,不等式f(x2-2x)+f(2y-y2)≤0成立,所以f(x2-2x)≥f(-2y+y2)成立,所以根據函數的單調性可得:對于任意的x,y∈R,不等式x2-2x≥y2-2y成立,即(x-y)(x+y-2)≥0(1≤x≤4),所以可得其可行域,如圖所示:
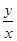 =
= 所以
所以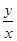 表示點(x,y)與點(0,0)連線的斜率,所以結合圖象可得:
表示點(x,y)與點(0,0)連線的斜率,所以結合圖象可得: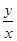 的最小值是直線OC的斜率-
的最小值是直線OC的斜率- ,最大值是直線AB的斜率1,所以
,最大值是直線AB的斜率1,所以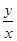 的范圍為:[
的范圍為:[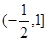 故答案為:
故答案為: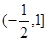


 課堂全解字詞句段篇章系列答案
課堂全解字詞句段篇章系列答案 步步高口算題卡系列答案
步步高口算題卡系列答案湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com