
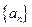 中,已知
中,已知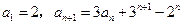
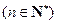 .
.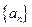 的通項公式;
的通項公式;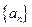 的前
的前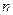 項和
項和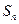 .
.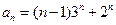
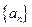 的前
的前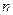 項和
項和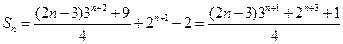
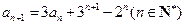
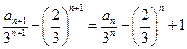 ,------------------------------3分
,------------------------------3分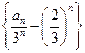 是首項為
是首項為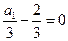 ,公差為1等差數列,
,公差為1等差數列,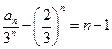 , -----------------6分
, -----------------6分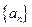 的通項公式為
的通項公式為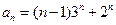 .-----------------------7分
.-----------------------7分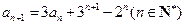
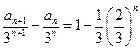 -------------------------2分
-------------------------2分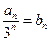 ,則
,則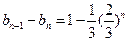 ---------------------3分
---------------------3分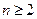 時
時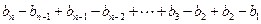
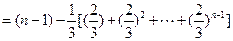 ----5分
----5分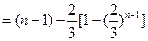
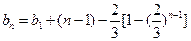
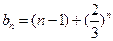 --------------------------------6分
--------------------------------6分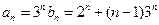 -------------------------------7分
-------------------------------7分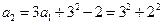 , -------------1分
, -------------1分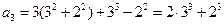 ,-----------------------------------2分
,-----------------------------------2分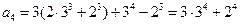 .---------------------------3分
.---------------------------3分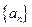 的通項公式為
的通項公式為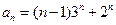 .----------------4分
.----------------4分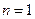 時,
時,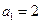 ,等式成立.
,等式成立.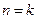 (
(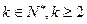 )時等式成立,即
)時等式成立,即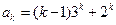 ,
,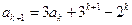
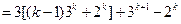
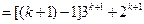 .--------------------------------6分
.--------------------------------6分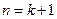 時等式也成立.根據①和②可知,等式
時等式也成立.根據①和②可知,等式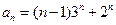 對任何
對任何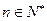 都成立.-------------------------------7分
都成立.-------------------------------7分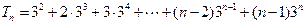 , ------①-----8分
, ------①-----8分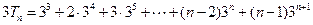 ------②------9分
------②------9分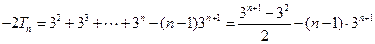 ,-------10分
,-------10分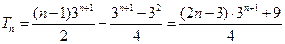 .------------------12分
.------------------12分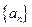 的前
的前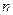 項和
項和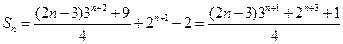


科目:高中數學 來源:不詳 題型:解答題
 的前n項和記為
的前n項和記為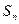 ,前
,前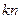 項和記為
項和記為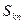
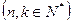 ,對給定的常數
,對給定的常數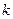 ,若
,若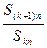 是與
是與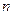 無關的非零常數
無關的非零常數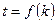 ,則稱該數列
,則稱該數列 是“
是“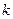 類和科比數列”,
類和科比數列”,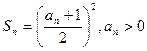 ,求數列
,求數列 的通項公式(5分);
的通項公式(5分);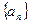 是一個 “
是一個 “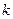 類和科比數列”(4分);
類和科比數列”(4分);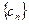 是一個等比數列,首項
是一個等比數列,首項 ,公比
,公比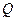
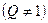 ,若數列
,若數列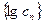 是一個 “
是一個 “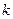 類和科比數列”,探究
類和科比數列”,探究 與
與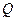 的關系(7分)
的關系(7分)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com