
(本題滿分14分)已知圓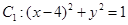 ,圓
,圓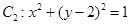 ,動點
,動點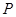 到圓
到圓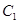 ,
,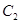 上點的距離的最小值相等.
上點的距離的最小值相等.
(1)求點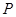 的軌跡方程;
的軌跡方程;
(2)點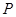 的軌跡上是否存在點
的軌跡上是否存在點 ,使得點
,使得點 到點
到點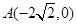 的距離減去點
的距離減去點 到點
到點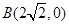 的距離的差為
的距離的差為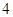 ,如果存在求出
,如果存在求出 點坐標,如果不存在說明理由.
點坐標,如果不存在說明理由.
(1)點 的軌跡方程是
的軌跡方程是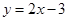 .(2)點
.(2)點 的軌跡上不存在滿足條件的點
的軌跡上不存在滿足條件的點 .
.
【解析】本試題主要是考查了動點的軌跡方程的求解,以及滿足動點到定點的距離差為定值的點是否存在的探索性問題的運用。
((1)根據已知設出點的坐標,因為點到圓上點的距離的最小值相等,所以可知點到圓心的距離相等,因此得到軌跡方程。
(2)假設存在點滿足題意可知,得到關于x,y的方程,然后利用方程有無解來判定是否存在的問題。
解:(1)設動點 的坐標為
的坐標為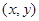 ,
,
圓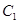 的圓心
的圓心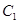 坐標為
坐標為 ,圓
,圓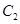 的圓心
的圓心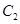 坐標為
坐標為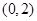 ,
,
因為動點 到圓
到圓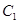 ,
,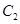 上的點距離最小值相等,所以
上的點距離最小值相等,所以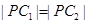 ,
,
即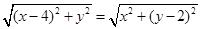 ,化簡得
,化簡得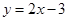 ,
,
因此點 的軌跡方程是
的軌跡方程是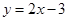 .
.
(2)假設這樣的 點存在,設點
點存在,設點
因為 點到
點到 點的距離減去
點的距離減去 點到
點到 點的距離的差為4,
點的距離的差為4,
所以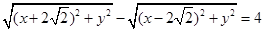 ,
,
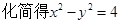 ,
,
又 點在直線
點在直線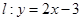 上,
上,  點的坐標是方程組
點的坐標是方程組 的解,
的解,
消元得 ,
,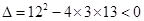 ,方程組無解,
,方程組無解,
所以點 的軌跡上不存在滿足條件的點
的軌跡上不存在滿足條件的點 .
.


 習題精選系列答案
習題精選系列答案科目:高中數學 來源:2012-2013學年吉林省高三第一次月考文科數學試卷(解析版) 題型:解答題
(本題滿分14分)已知函數
(1)若 ,求x的值;
,求x的值;
(2)若 對于
對于 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
(本題滿分14分)
已知橢圓 :
: 的離心率為
的離心率為 ,過坐標原點
,過坐標原點 且斜率為
且斜率為 的直線
的直線 與
與 相交于
相交于 、
、 ,
, .
.
⑴求 、
、 的值;
的值;
⑵若動圓 與橢圓
與橢圓 和直線
和直線 都沒有公共點,試求
都沒有公共點,試求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
((本題滿分14分)
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
(1)當x=2時,求證:BD⊥EG ;
(2)若以F、B、C、D為頂點的三棱錐的體積記為 ,
,
求 的最大值;
的最大值;


(3)當 取得最大值時,求二面角D-BF-C的余弦值.
取得最大值時,求二面角D-BF-C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com