

 在區間
在區間 上的最大值
上的最大值
 使得
使得 的圖象與
的圖象與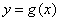 的圖象有且只有三個不同的交點?若存在,求出
的圖象有且只有三個不同的交點?若存在,求出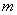 的取值范圍;若不存在,說明理由。
的取值范圍;若不存在,說明理由。科目:高中數學 來源:不詳 題型:解答題
 )
)
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
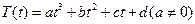 ,其中溫度的單位是℃,時間的單位是小時.中午12:00相應的t=0,中午12:00以后相應的t取正數,中午12:00以前相應的t取負數(如早上8:00相應的t=-4,下午16:00相應的t=4).若測得該物體在早上8:00的溫度為8℃,中午12:00的溫度為60℃,下午13:00的溫度為58℃,且已知該物體的溫度早上8:00與下午16:00有相同的變化率.
,其中溫度的單位是℃,時間的單位是小時.中午12:00相應的t=0,中午12:00以后相應的t取正數,中午12:00以前相應的t取負數(如早上8:00相應的t=-4,下午16:00相應的t=4).若測得該物體在早上8:00的溫度為8℃,中午12:00的溫度為60℃,下午13:00的溫度為58℃,且已知該物體的溫度早上8:00與下午16:00有相同的變化率.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com