等差數列{an}中,已知a1=3,a4=12,
(I)求數列{an}的通項公式;
(Ⅱ)若a2,a4分別為等比數列{bn}的第1項和第2項,試求數列{bn}的通項公式及前n項和Sn.
解:(I)設數列{a
n}的公差為d,
由已知有

(2分)
解得d=3(4分)
∴a
n=3+(n-1)3=3n(6分)
(Ⅱ)由(I)得a
2=6,a
4=12,則b
1=6,b
2=12,(8分)
設b
n的公比為q,則
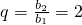
,(9分)
從而b
n=6•2
n-1=3•2
n(11分)
所以數列{b
n}的前n項和
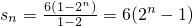
(12分)
分析:(I)求數列{a
n}的通項公式,由等差數列{a
n}中,已知a
1=3,a
4=12,先求出公差d,再依據等差數列的通項公式求其通項即可.
(Ⅱ)若a
2,a
4分別為等比數列{b
n}的第1項和第2項,由此即可求出等比數列的首項與公比,再由公式求出其通項公式及前n項和S
n.
點評:本題考查等差數列與等比數列的綜合,熟知等差數列與等比數列的性質是求解本題的關鍵,本題屬于考查基本公式型的題,思維難度相對較低.

 (2分)
(2分)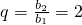 ,(9分)
,(9分)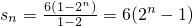 (12分)
(12分)
