Question

（2013年四川攀枝花8分）如圖，PA為⊙O的切線，A為切點，直線PO交⊙O與點E，F過點A作PO的垂線AB垂足為D，交⊙O與點B，延長BO與⊙O交與點C，連接AC，BF．

（1）求證：PB與⊙O相切；

（2）試探究線段EF，OD，OP之間的數量關系，并加以證明；

（3）若AC=12，tan∠F=，求cos∠ACB的值．

 

Answer 1

【答案】

解：（1）證明：連接OA，

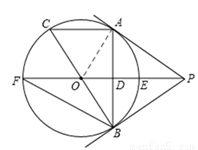
∵PA與⊙O相切，

∴PA⊥OA，即∠OAP=90°。

∵OP⊥AB，∴D為AB中點，即OP垂直平分AB

∴PA=PB。

∵在△OAP和△OBP中，，

∴△OAP≌△OBP（SSS）。

∴∠OAP=∠OBP=90°。∴BP⊥OB。

∵OB是⊙O的半徑，∴PB為圓O的切線。

（2）EF²=4DO•PO。證明如下：

∵∠OAP=∠ADO=90°，∠AOD=∠POA，∴△OAD∽△OPA。

∴，即OA²=OD•OP。

∵EF為圓的直徑，即EF=2OA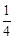，∴EF²=OD•OP，即EF²=4OD•OP。

（3）連接BE，則∠FBE=90°。

∵tan∠F=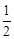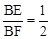，∴。∴可設BE=x，BF=2x。

則由勾股定理，得。

∵S_△BEF=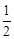BE•BF=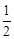EF•BD，∴BD=。

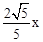又∵AB⊥EF，∴AB=2BD=。

∴Rt△ABC中，BC=，AC²+AB²=BC²，

∴12²+（）²=（）²，解得：x=。

∴BC=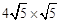=20。

∴。

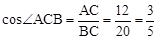【解析】（1）連接OA，由OP垂直于AB，利用垂徑定理得到D為AB的中點，即OP垂直平分AB，可得出AP=BP，再由OA=OB，OP=OP，利用SSS得出三角形AOP與三角形BOP全等，由PA為圓的切線，得到OA垂直于AP，利用全等三角形的對應角相等及垂直的定義得到OB垂直于BP，即PB為圓O的切線。

（2）由一對直角相等，一對公共角，得出三角形AOD與三角形OAP相似，由相似得比例，列出關系式，由OA為EF的一半，等量代換即可得證。

（3）連接BE，構建直角△BEF．在該直角三角形中利用銳角三角函數的定義、勾股定理可設BE=x，BF=2x，進而可得EF=；然后由面積法求得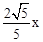，所以根據垂徑定理求得AB的長度，在Rt△ABC中，根據勾股定理易求BC的長；最后由余弦三角函數的定義求解。

考點：圓的綜合題，切線的判定和性質，圓周角定理，垂徑定理，全等三角形的判定和性質，相似三角形的判定和性質，銳角三角函數定義，勾股定理，三角形面積法的應用。