Question

已知直線，直線與、分別交于、兩點，點是直線上的一動點
如圖，若動點在線段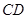之間運動（不與、兩點重合），問在點的運動過程中是否始終具有這一相等關系？試說明理由；
如圖，當動點在線段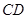之外且在的上方運動（不與、兩點重合），則上述結論是否仍成立？若不成立，試寫出新的結論，并說明理由；

Answer 1

（1）∠3+∠1=∠2成立，理由見解析；（2）∠3+∠1=∠2不成立，新的結論為∠3-∠1=∠2．

解析試題分析：（1）相等關系成立．過點P作PE∥l₁，則有∠1=∠APE，又因為PE∥l₂，又有∠3=∠BPE，因為∠BPE+∠APE=∠2，所以∠3+∠1=∠2；
（2）原關系不成立，過點P作PE∥l₁，則有∠1=∠APE；又因為PE∥l₂，又有∠3=∠BPE，困為此時∠BPE-∠APE=∠2，則有∠3-∠1=∠2．
（1）∠3+∠1=∠2成立．
理由如下：
過點P作PE∥l₁，
∴∠1=∠APE；
∵l₁∥l₂，
∴PE∥l₂，
∴∠3=∠BPE；
又∵∠BPE+∠APE=∠2，
∴∠3+∠1=∠2．

（2）∠3+∠1=∠2不成立，新的結論為∠3-∠1=∠2．
理由如下：
過點P作PE∥l₁，
∴∠1=∠APE；
∵l₁∥l₂，
∴PE∥l₂，
∴∠3=∠BPE；
又∵∠BPE-∠APE=∠2，
∴∠3-∠1=∠2．
考點：平行線的性質．