
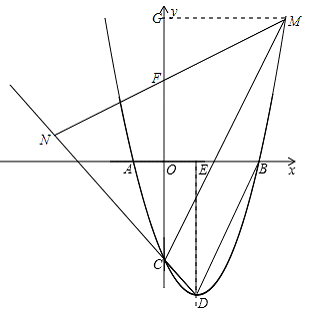
 與x軸交于A,B兩點(點A在點B左側),與y軸交于點C,點D為頂點.
與x軸交于A,B兩點(點A在點B左側),與y軸交于點C,點D為頂點.
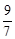 ,
,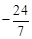 )②點M坐標為(
)②點M坐標為(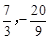 )或(5,12)
)或(5,12) 與x軸交于A,B兩點(點A在點B左側),
與x軸交于A,B兩點(點A在點B左側),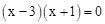 ,解得x=3或x=﹣1。∴點B的坐標為(3,0)。
,解得x=3或x=﹣1。∴點B的坐標為(3,0)。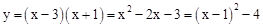 ,∴頂點D的坐標為(1,-4)。
,∴頂點D的坐標為(1,-4)。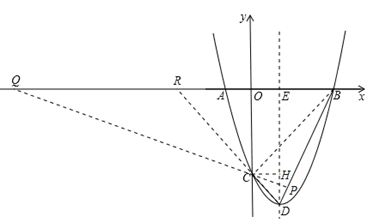
 與y軸交于點C,
與y軸交于點C,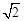 ,CB=3
,CB=3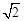 ,△BCD為直角三角形。
,△BCD為直角三角形。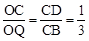 。
。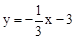 。
。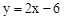 ,
,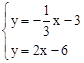 解得:
解得: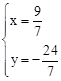 。
。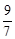 ,
,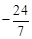 )。
)。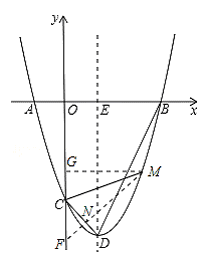
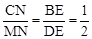 。∴MN=2CN。
。∴MN=2CN。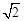 a。∴MF=MN+NF=3a。∴MG=FG=
a。∴MF=MN+NF=3a。∴MG=FG=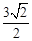 a。
a。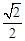 a。
a。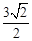 a,
a, )。
)。 ,解得a=
,解得a=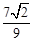 。,
。,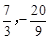 )。
)。
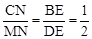 。
。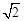 a。
a。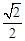 a。∴CG=FG+FC=
a。∴CG=FG+FC=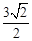 a。∴M(
a。∴M(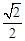 a,
a,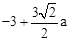 )。
)。 ,解得a=
,解得a=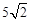 。
。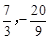 )或(5,12)。
)或(5,12)。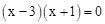 ,求出x=3或﹣1,根據拋物線
,求出x=3或﹣1,根據拋物線 與x軸交于A,B兩點(點A在點B左側),確定點B的坐標為(3,0);將拋物線寫成頂點式
與x軸交于A,B兩點(點A在點B左側),確定點B的坐標為(3,0);將拋物線寫成頂點式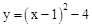 ,即可確定頂點D的坐標。
,即可確定頂點D的坐標。 ,得到點C、點E的坐標.連接BC,過點C作CH⊥DE于H,由勾股定理得出CD=
,得到點C、點E的坐標.連接BC,過點C作CH⊥DE于H,由勾股定理得出CD=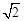 ,CB=3
,CB=3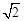 ,證明△BCD為直角三角形.分別延長PC、DC,與x軸相交于點Q,R.根據兩角對應相等的兩三角形相似證明△BCD∽△QOC,則
,證明△BCD為直角三角形.分別延長PC、DC,與x軸相交于點Q,R.根據兩角對應相等的兩三角形相似證明△BCD∽△QOC,則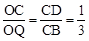 ,得出Q的坐標(﹣9,0),運用待定系數法求出直線CQ的解析式為
,得出Q的坐標(﹣9,0),運用待定系數法求出直線CQ的解析式為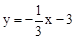 ,直線BD的解析式為
,直線BD的解析式為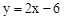 ,解方程組
,解方程組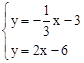 ,即可求出點P的坐標。
,即可求出點P的坐標。

科目:初中數學 來源:不詳 題型:解答題

 .
.查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
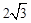 ,若以O為坐標原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.
,若以O為坐標原點,OA所在直線為x軸,建立如圖所示的平面直角坐標系,點B在第一象限內,將Rt△OAB沿OB折疊后,點A落在第一象限內的點C處.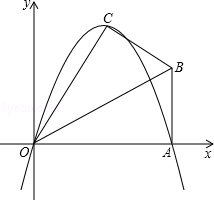
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
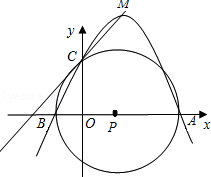
查看答案和解析>>
科目:初中數學 來源:不詳 題型:單選題
| A.3 | B.5 | C.7 | D.不確定 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com