
提出問題:如圖①,在四邊形ABCD中,點E、F是AD的n等分點中最中間2個,點G、H是BC的n等分點中最中間2個,(其中n為奇數),連接EG、FH,那么S四邊形EFHG與S四邊形ABCD之間有什么關系呢?
探究發現:為了解決這個問題,我們可以先從一些簡單的、特殊的情形入手:
(1)如圖②:四邊形ABCD中,點E、F是AD的3等分點,點G、H是BC的3等分點,連接EG、FH,那么S四邊形EFHG與S四邊形ABCD之間有什么關系呢?
如圖③,連接EH、BE、DH,
因為△EGH與△EBH高相等,底的比是1:2,
所以S△EGH= S△EBH
S△EBH
因為△EFH與△DEH高相等,底的比是1:2,
所以S△EFH= S△DEH
S△DEH
所以S△EGH+S△EFH= S△EBH +
S△EBH + S△DEH
S△DEH
即S四邊形EFHG= S四邊形EBHD
S四邊形EBHD
連接BD,
因為△DBE與△ABD高相等,底的比是2:3,
所以S△DBE= S△ABD
S△ABD
因為△BDH與△BCD高相等,底的比是2:3,
所以S△BDH= S△BCD
S△BCD
所以S△DBE +S△BDH= S△ABD+
S△ABD+ S△BCD =
S△BCD = (S△ABD+S△BCD)
(S△ABD+S△BCD)
= S四邊形ABCD
S四邊形ABCD
即S四邊形EBHD= S四邊形ABCD
S四邊形ABCD
所以S四邊形EFHG= S四邊形EBHD=
S四邊形EBHD= ×
× S四邊形ABCD=
S四邊形ABCD= S四邊形ABCD
S四邊形ABCD
(1)如圖④:四邊形ABCD中,點E、F是AD的5等分點中最中間2個,點G、H是BC的5等分點中最中間2個,連接EG、FH,猜想:S四邊形EFHG與S四邊形ABCD之間有什么關系呢
驗證你的猜想:
(2)問題解決:如圖①,在四邊形ABCD中,點E、F是AD的n等分點中最中間2個,點G、H是BC的n等分點中最中間2個,連接EG、FH,(其中n為奇數)
那么S四邊形EFHG與S四邊形ABCD之間的關系為: (不必寫出求解過程)
(1)S四邊形EFHG=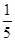 S四邊形ABCD,證明見解析;
S四邊形ABCD,證明見解析;
(2)S四邊形EFHG=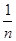 S四邊形ABCD.
S四邊形ABCD.
解析試題分析:仿照上面的探究思路,類比求解.
試題解析:(1)四邊形ABCD中,點E、F是AD的5等分點中最中間2個,點G、H是BC的5等分點中最中間2個,連接EG、FH,S四邊形EFHG=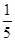 S四邊形ABCD,
S四邊形ABCD,
如圖④:連接EH、BE、DH,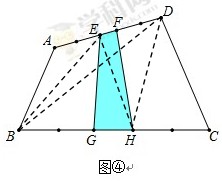
因為△EGH與△EBH高相等,底的比是1:3,
所以S△EGH= S△EBH
S△EBH
因為△EFH與△DEH高相等,底的比是1:3,
所以S△EFH= S△DEH
S△DEH
所以S△EGH+S△EFH= S△EBH +
S△EBH + S△DEH
S△DEH
即S四邊形EFHG= S四邊形EBHD
S四邊形EBHD
連接BD,
因為△DBE與△ABD高相等,底的比是3:5,
所以S△DBE=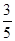 S△ABD
S△ABD
因為△BDH與△BCD高相等,底的比是3:5,
所以S△BDH=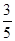 S△BCD
S△BCD
所以S△DBE +S△BDH=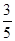 S△ABD+
S△ABD+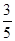 S△BCD =
S△BCD =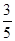 (S△ABD+S△BCD)
(S△ABD+S△BCD)
=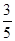 S四邊形ABCD
S四邊形ABCD
即S四邊形EBHD=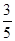 S四邊形ABCD
S四邊形ABCD
所以S四邊形EFHG= S四邊形EBHD=
S四邊形EBHD= ×
×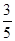 S四邊形ABCD=
S四邊形ABCD=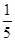 S四邊形ABCD.
S四邊形ABCD.
(2)在四邊形ABCD中,點E、F是AD的n等分點中最中間2個,點G、H是BC的n等分點中最中間2個,連接EG、FH,(其中n為奇數)那么S四邊形EFHG=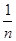 S四邊形ABCD.
S四邊形ABCD.
考點:三角形的面積.


科目:初中數學 來源: 題型:解答題
在□ABCD中,AE、BF分別平分∠DAB和∠ABC,交CD于點E、F,AE、BF相交于點M.
(1)試說明:AE⊥BF;
(2)判斷線段DF與CE的大小關系,并說明理由.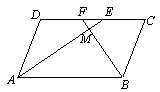
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
已知:Rt△OAB在直角坐標系中的位置如圖所示,P(3,4)為OB的中點,點C為折線OAB上的動點,線段PC把Rt△OAB分割成兩部分. 問:點C在什么位置時,分割得到的三角形與Rt△OAB相似?(注:在圖上畫出所有符合要求的線段PC,并寫出相應的點C的坐標).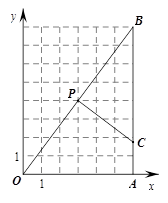
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,△ABC與△A′B′C′是位似圖形,且頂點都在格點上,每個小正方形的邊長都為1.
(1)在圖上標出位似中心D的位置,并寫出該位似中心D的坐標是 ;
(2)求△ABC與△A′B′C′的面積比.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
為了測量校園水平地面上一棵樹的高度,數學興趣小組利用一根標桿、皮尺,設計如圖所示的測量方案.已知測量同學眼睛A、標桿頂端F、樹的頂端E在同一直線上,此同學眼睛距地面1.6米,標桿為3.1米,且BC=1米,CD=5米,請你根據所給出的數據求樹高ED.
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
如圖,在平行四邊形ABCD中,過點A作AE⊥BC,垂足為E,連接DE,F為線段DE上一點,且∠AFE=∠B.
(1)求證:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的長.
,求AE的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com