
閱讀材料:若a,b都是非負實數,則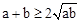 .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
證明:∵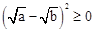 ,∴
,∴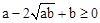 .
.
∴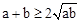 .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
舉例應用:已知x>0,求函數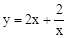 的最小值.
的最小值.
解: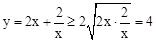 .當且僅當
.當且僅當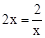 ,即x=1時,“=”成立.
,即x=1時,“=”成立.
當x=1時,函數取得最小值,y最小=4.
問題解決:汽車的經濟時速是指汽車最省油的行駛速度.某種汽車在每小時70~110公里之間行駛時(含70公里和110公里),每公里耗油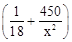 升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.
升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.
(1)求y關于x的函數關系式(寫出自變量x的取值范圍);
(2)求該汽車的經濟時速及經濟時速的百公里耗油量(結果保留小數點后一位).
 小學期末沖刺100分系列答案
小學期末沖刺100分系列答案 期末復習檢測系列答案
期末復習檢測系列答案 超能學典單元期中期末專題沖刺100分系列答案
超能學典單元期中期末專題沖刺100分系列答案 黃岡360度定制密卷系列答案
黃岡360度定制密卷系列答案科目:初中數學 來源: 題型:閱讀理解
| ab |
| a |
| b |
| ab |
| ab |
| 2 |
| x |
| 2 |
| x |
2x•
|
| 2 |
| x |
| 1 |
| 18 |
| 450 |
| x2 |
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
閱讀材料:若a,b都是非負實數,則![]() .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
證明:∵![]() ,∴
,∴![]() .
.
∴![]() .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
舉例應用:已知x>0,求函數![]() 的最小值.
的最小值.
解:![]() .當且僅當
.當且僅當![]() ,即x=1時,“=”成立.
,即x=1時,“=”成立.
當x=1時,函數取得最小值,y最小=4.
問題解決:汽車的經濟時速是指汽車最省油的行駛速度.某種汽車在每小時70~110公里之間行駛時(含70公里和110公里),每公里耗油![]() 升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.
升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.
(1)求y關于x的函數關系式(寫出自變量x的取值范圍);
(2)求該汽車的經濟時速及經濟時速的百公里耗油量(結果保留小數點后一位).
查看答案和解析>>
科目:初中數學 來源: 題型:閱讀理解
閱讀材料:若a,b都是非負實數,則![]() .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
證明:∵![]() ,∴
,∴![]() .
.
∴![]() .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
舉例應用:已知x>0,求函數![]() 的最小值.
的最小值.
解:![]() .當且僅當
.當且僅當![]() ,即x=1時,“=”成立.
,即x=1時,“=”成立.
當x=1時,函數取得最小值,y最小=4.
問題解決:汽車的經濟時速是指汽車最省油的行駛速度.某種汽車在每小時70~110公里之間行駛時(含70公里和110公里),每公里耗油![]() 升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.
升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.
(1)求y關于x的函數關系式(寫出自變量x的取值范圍);
(2)求該汽車的經濟時速及經濟時速的百公里耗油量(結果保留小數點后一位).
查看答案和解析>>
科目:初中數學 來源:2013年山東省濟寧市中考數學試卷(解析版) 題型:解答題
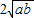 .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.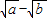 )2≥0,∴a-
)2≥0,∴a-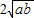 +b≥0.
+b≥0.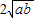 .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.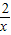 的最小值.
的最小值.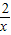 ≥
≥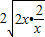 =4.當且僅當2x=
=4.當且僅當2x=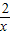 ,即x=1時,“=”成立.
,即x=1時,“=”成立.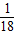 +
+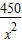 )升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.
)升.若該汽車以每小時x公里的速度勻速行駛,1小時的耗油量為y升.查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com