精英家教網> 2025年多維互動提優課堂九年級數學上冊蘇科版提升版 > 第1頁 參考答案
2025年多維互動提優課堂九年級數學上冊蘇科版提升版
注:目前有些書本章節名稱可能整理的還不是很完善,但都是按照順序排列的,請同學們按照順序仔細查找。練習冊2025年多維互動提優課堂九年級數學上冊蘇科版提升版答案主要是用來給同學們做完題方便對答案用的,請勿直接抄襲。
1. 下列方程屬于一元二次方程的是 (
B
)
A.$2xy - 7 = 0$
B.$x^2 - 7 = 0$
C.$-7x = 0$
D.$5(x + 1) = 7^2$
答案:【解析】:
本題主要考察一元二次方程的定義,即只含有一個未知數,且未知數的最高次數為2的整式方程。
A選項:$2xy - 7 = 0$,此方程含有兩個未知數x和y,因此不是一元二次方程。
B選項:$x^2 - 7 = 0$,此方程只含有一個未知數x,且x的最高次數為2,滿足一元二次方程的定義。
C選項:$-7x = 0$,此方程只含有一個未知數x,但x的最高次數為1,因此不是一元二次方程。
D選項:$5(x + 1) = 7^2$,展開后為$5x + 5 = 49$,此方程只含有一個未知數x,但x的最高次數為1,因此不是一元二次方程。
【答案】:
B
2. 方程$2x^2 - 3x = 2$的一次項系數和常數項分別是 (
D
)
A.2和2
B.$-3$和2
C.3和$-2$
D.$-3和-2$
答案:【解析】:
本題考查一元二次方程的一般形式,即$ax^2 + bx + c = 0$(其中$a \neq 0$)的形式。
在這個形式中,$ax^2$是二次項,$bx$是一次項,$c$是常數項。
題目給出的方程是$2x^2 - 3x = 2$,為了找到一次項系數和常數項,需要先將方程化為一般形式。
將方程$2x^2 - 3x = 2$移項,得到$2x^2 - 3x - 2 = 0$。
在這個一般形式中,可以清晰地看到一次項系數是$-3$,常數項是$-2$。
【答案】:
D. $-3$和$-2$。
3. 若關于$x的一元二次方程(x - a)^2 - 4 = b$有實數根,則$b$的取值范圍是 (
D
)
A.$b > 4$
B.$b > -4$
C.$b \geq 4$
D.$b \geq -4$
答案:解:$(x - a)^2 - 4 = b$
移項得$(x - a)^2 = b + 4$
∵一元二次方程有實數根,
∴$(x - a)^2 \geq 0$
即$b + 4 \geq 0$
解得$b \geq -4$
D
4. 若$x$為任意有理數,則多項式$4x - 4 - x^2$的值 (
C
)
A.一定為正數
B.一定為負數
C.不可能為正數
D.可能為任意有理數
答案:【解析】:
首先,我們將多項式$4x - 4 - x^2$進行整理,得到:
$4x - 4 - x^2 = - (x^2 - 4x + 4) = - (x - 2)^2$
由于$(x - 2)^2$是一個平方項,其值總是非負的,即:
$(x - 2)^2 \geq 0$
因此,$- (x - 2)^2$的值總是非正的,即:
$- (x - 2)^2 \leq 0$
所以多項式$4x - 4 - x^2$的值不可能為正數。
【答案】:
C. 不可能為正數。
5. 若關于$x的一元二次方程ax^2 + bx + 1 = 0$的一個根是1,則$2024 - a - b$的值是 (
A
)
A.2025
B.2023
C.2024
D.2022
答案:解:
∵關于$x$的一元二次方程$ax^2 + bx + 1 = 0$的一個根是$1$,
∴將$x = 1$代入方程得:$a×1^2 + b×1 + 1 = 0$,
即$a + b + 1 = 0$,
∴$a + b = -1$,
則$2024 - a - b = 2024 - (a + b) = 2024 - (-1) = 2025$。
A
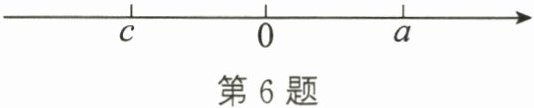
6. 已知關于$x的一元二次方程ax^2 - x + c = 0$,其中$a$,$c$在數軸上的對應點的位置如圖所示,則這個方程的根的情況是 (
C
)
A.沒有實數根
B.有兩個相等的實數根
C.有兩個不相等的實數根
D.無法確定
答案:解:由數軸可知,$a > 0$,$c < 0$。
對于一元二次方程$ax^2 - x + c = 0$,判別式$\Delta = (-1)^2 - 4ac = 1 - 4ac$。
因為$a > 0$,$c < 0$,所以$ac < 0$,則$-4ac > 0$,故$\Delta = 1 - 4ac > 1 > 0$。
所以方程有兩個不相等的實數根。
答案:C
7. 把一根長為2 m的繩子分成兩段,使較長一段的長的平方等于較短一段的長與原繩長的積. 設較長一段的長為$x$ m,根據題意,可列方程為 (
A
)
A.$x^2 = 2(2 - x)$
B.$x^2 = 2(2 + x)$
C.$(2 - x)^2 = 2x$
D.$x^2 = 2 - x$
答案:解:設較長一段的長為$x$m,則較短一段的長為$(2 - x)$m。
根據題意,較長一段的長的平方等于較短一段的長與原繩長的積,可列方程為:$x^2 = 2(2 - x)$。
答案:A
8. 已知實數a,b,且$a \neq b,$又a,b滿足$a^2 = 3a + 1,b^2 = 3b + 1,$則$a^2 + b^2$的值為 (
C
)
A.9
B.10
C.11
D.12
答案:【解析】:
本題主要考查了一元二次方程的根與系數的關系以及代數式的化簡。
根據題目條件,$a$ 和 $b$ 是方程 $x^2 - 3x - 1 = 0$ 的兩個不相等的實數根。
根據一元二次方程的根與系數的關系,我們有:
根的和:$a + b = -\frac{-3}{1} = 3$,
根的積:$ab = \frac{-1}{1} = -1$,
接下來,我們需要求 $a^2 + b^2$ 的值。
根據平方和公式,我們有:
$a^2 + b^2 = (a + b)^2 - 2ab$,
將 $a + b = 3$ 和 $ab = -1$ 代入上式,得到:
$a^2 + b^2 = 3^2 - 2 × (-1) = 9 + 2 = 11$。
【答案】:
C. $11$。

