
(本小題滿分14分)
如圖,已知幾何體的三視圖(單位:cm).
(1)在這個幾何體的直觀圖相應的位置標出字母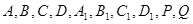 ;(2分)
;(2分)
(2)求這個幾何體的表面積及體積;(6分)
(3)設異面直線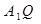 、
、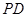 所成角為
所成角為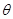 ,求
,求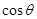 .(6分)
.(6分)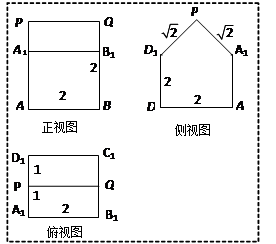

解(1)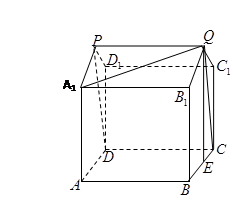
(2)幾何體的全面積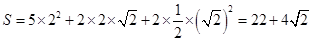
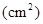 ;
;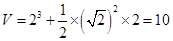
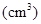 ;
;
(3異面直線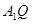 、
、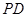 所成角的余弦值為
所成角的余弦值為 .
.
解析試題分析:(1)根據(jù)三視圖的畫出,進行復原畫出幾何體的圖形即可.
(2)幾何體可看成是正方體AC1及直三棱柱B1C1Q-A1D1P的組合體,求出底面面積,然后求出體積即可.
(3)通過建立空間直角坐標系求解也可以,也能通過平移法得到異面直線的所成的角的大小,進而解得。
解(1)幾何體的直觀圖相應的位置標出字母如圖所示.…………2分 
(2)這個幾何體可看成是由正方體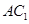 及直三棱柱
及直三棱柱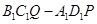 的組合體.
的組合體.
由 ,
,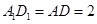 ,可得
,可得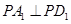 .
.
故所求幾何體的全面積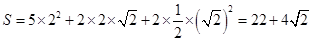
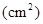 …5分
…5分
所求幾何體的體積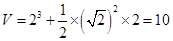
 ……8分
……8分
(3)由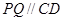 ,且
,且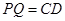 ,可知
,可知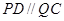 ,
,
故 為異面直線
為異面直線 、
、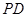 所成的角(或其補角).……10分
所成的角(或其補角).……10分
由題設知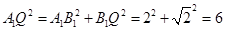 ,
,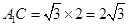 ,
,
取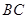 中點
中點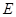 ,則
,則 ,且
,且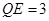 ,
, .……12分
.……12分
由余弦定理,得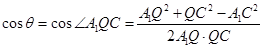
 .……13分
.……13分
所以異面直線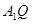 、
、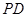 所成角的余弦值為
所成角的余弦值為 .………………14分
.………………14分
考點:本試題主要考查了三視圖復原幾何體,畫出中逐步按照三視圖的作法復原,考查空間想象能力,邏輯推理能力,計算能力,轉化思想,是中檔題.
點評:解決該試題的關鍵是能準確的由三視圖得到原幾何體,并能結合棱柱的體積和表面積公式準確運算,考查了一定的計算能力。


 一諾書業(yè)暑假作業(yè)快樂假期云南美術出版社系列答案
一諾書業(yè)暑假作業(yè)快樂假期云南美術出版社系列答案科目:高中數(shù)學 來源: 題型:解答題
(本小題滿分12分)如圖 ,已知在四棱錐
,已知在四棱錐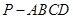 中,底面
中,底面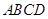 是矩形,
是矩形,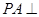 平面
平面 ,
, ,
, ,
,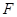 是
是 的中點,
的中點,  是線段
是線段 上的點.
上的點.
(I)當 是
是 的中點時,求證:
的中點時,求證: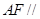 平面
平面 ;
;
(II)要使二面角 的大小為
的大小為 ,試確定
,試確定 點的位置.
點的位置.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(本小題滿分12分)右圖是一個直三棱柱(以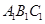 為底面)被一平面所截得到的幾何體,截面為
為底面)被一平面所截得到的幾何體,截面為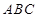 已知
已知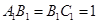 ,
,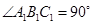 ,
,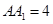 ,
,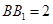 ,
,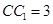

(Ⅰ)設點 是
是 的中點,證明:
的中點,證明: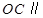 平面
平面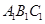 ;
;
(Ⅱ)求二面角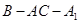 的大小;
的大小;
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(本小題滿分12分) 如圖,在四棱錐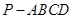 中,底面
中,底面 是正方形,側棱
是正方形,側棱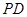 ⊥底面
⊥底面 ,
, ,
, 是
是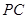 的中點,作
的中點,作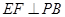 交
交 于點
于點
(1) 證明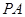 //平面
//平面 ;
;
(2) 證明 ⊥平面
⊥平面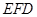 ;
;
(3) 求二面角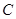 —
— —
—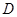 的大小。
的大小。
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
(20) (本題滿分14分) 已知正四棱錐P-ABCD中,底面是邊長為2 的正方形,高為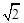 .M為線段PC的中點.
.M為線段PC的中點.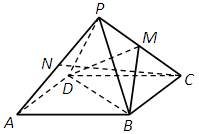
(Ⅰ) 求證:PA∥平面MDB;
(Ⅱ) N為AP的中點,求CN與平面MBD所成角的正切值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:解答題
如圖所示,在長方體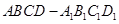 中,
中,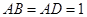 ,
,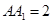 ,
,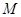 是棱
是棱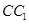 上一點,
上一點,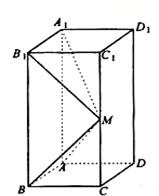
(1)若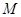 為CC1的中點,求異面直線A1M和C1D1所成的角的正切值;
為CC1的中點,求異面直線A1M和C1D1所成的角的正切值;
(2)是否存在這樣的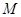 ,使得平面ABM⊥平面A1B1M,若存在,求出
,使得平面ABM⊥平面A1B1M,若存在,求出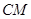 的值;若不存在,請說明理由。
的值;若不存在,請說明理由。
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com