
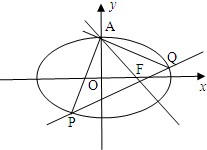
如圖,已知橢圓C: +
+ =1(a>b>0)的左、右焦點分別為F
=1(a>b>0)的左、右焦點分別為F 、F
、F ,A是橢圓C上的一點,AF
,A是橢圓C上的一點,AF ⊥F
⊥F F
F ,O是坐標原點,OB垂直AF
,O是坐標原點,OB垂直AF 于B,且OF
于B,且OF =3OB.
=3OB.

(Ⅰ)求橢圓C的離心率;
(Ⅱ)求t∈(0,b),使得命題“設圓x +y
+y =t
=t 上任意點M(x
上任意點M(x ,y
,y )處的切線交橢圓C于Q
)處的切線交橢圓C于Q 、Q
、Q 兩點,那么OQ
兩點,那么OQ ⊥OQ
⊥OQ ”成立.
”成立.
(1)橢圓C的離心率為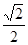 . (2)t=
. (2)t= b∈(0,b)使得所述命題成
b∈(0,b)使得所述命題成
【解析】
試題分析:解:(Ⅰ)解法一:由題設AF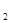 ⊥F
⊥F F
F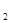 及F
及F (-c,0),F
(-c,0),F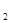 (c,0),不妨設點A(c,y),其中y>0,由于點A在橢圓上,有
(c,0),不妨設點A(c,y),其中y>0,由于點A在橢圓上,有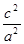 +
+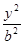 =1,
=1,
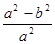 +
+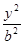 =1,解得y=
=1,解得y=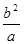 ,從而得到A
,從而得到A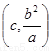 .
1分
.
1分
直線AF 的方程為y=
的方程為y= (x+c),整理得b
(x+c),整理得b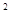 x-2acy+b
x-2acy+b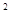 c=0. 2分
c=0. 2分
由題設,原點O到直線AF 的距離為
的距離為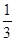 |OF
|OF |,即
|,即 =
=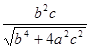 , 3分
, 3分
將c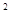 =a
=a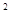 -b
-b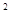 代入原式并化簡得a
代入原式并化簡得a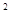 =2b
=2b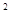 ,即a=
,即a= b.
b.
∴e= =
=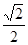 .即橢圓C的離心率為
.即橢圓C的離心率為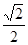 .
4分
.
4分
解法二:點A的坐標為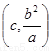 .
1分
.
1分
過點O作OB⊥AF ,垂足為B,易知△F
,垂足為B,易知△F BC∽△F
BC∽△F F
F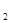 A,
A,
故 =
=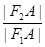 .
2分
.
2分
由橢圓定義得|AF |+|AF
|+|AF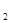 |=2a,又|BO|=
|=2a,又|BO|=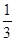 |OF
|OF |,
|,
所以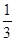
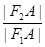 =
=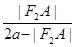 .
3分
.
3分
解得|F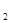 A|=
A|=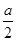 ,而|F
,而|F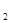 A|=
A|=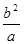 ,得
,得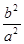 =
= .
.
∴e= =
=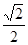 .即橢圓C的離心率為
.即橢圓C的離心率為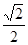 .
4分
.
4分
(Ⅱ)圓x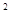 +y
+y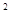 =t
=t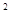 上的任意點M(x
上的任意點M(x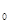 ,y
,y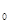 )處的切線方程為x
)處的切線方程為x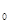 x+y
x+y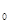 y=t
y=t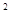 . 5分
. 5分
當t∈(0,b)時,圓x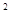 +y
+y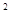 =t
=t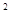 上的任意點都在橢圓內,故此圓在點A處的切線必交橢圓于兩個不同的點Q
上的任意點都在橢圓內,故此圓在點A處的切線必交橢圓于兩個不同的點Q 、Q
、Q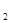 ,因此點Q
,因此點Q (x
(x ,y
,y ),Q
),Q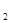 (x
(x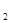 ,y
,y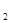 )的坐標是方程組
)的坐標是方程組
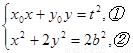 的解.
6分
的解.
6分
(1)當y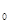
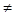 0時,由①式得y=
0時,由①式得y=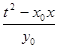 .代入②式,得x
.代入②式,得x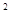 +2
+2 =2b
=2b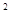 ,
,
即(2x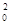 +y
+y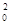 )x
)x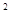 -4t
-4t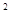 x
x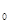 x+2t
x+2t -2b
-2b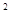 y
y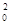 =0.
7分
=0.
7分
于是x +x
+x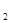 =
= ,x
,x x
x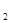 =
=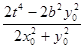 ,
,
y y
y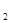 =
=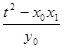 ·
·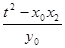 =
=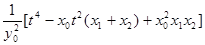
=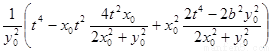 =
=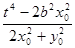 .
.
若QQ ⊥QQ
⊥QQ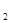 ,則x
,則x x
x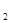 + y
+ y y
y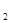 =
=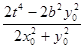 +
+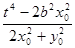 =
= =0.
=0.
所以,3t -2b
-2b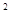 (x
(x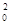 +y
+y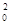 )=0. 8分
)=0. 8分
在區間(0,b)內,此方程的解為t= b.
9分
b.
9分
(2)當y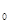 =0時,必有x
=0時,必有x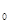
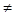 0,
0,
同理求得在區間(0,b)內的解為t= b.
10分
b.
10分
另一方面,當t= b時,可推出x
b時,可推出x x
x + y
+ y y
y =0,從而QQ
=0,從而QQ ⊥QQ
⊥QQ . 11分
. 11分
綜上所述,t= b∈(0,b)使得所述命題成立.
12分
b∈(0,b)使得所述命題成立.
12分
考點:橢圓的方程與性質
點評:解決的關鍵是熟練的根據橢圓的性質來求解方程,同時借助與聯立方程組的思想和韋達定理來表示得到參數的取值范圍,屬于中檔題。


科目:高中數學 來源: 題型:
 如圖,已知橢圓C:
如圖,已知橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| x2 |
| 4 |
| x2 |
| 16 |
| y2 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
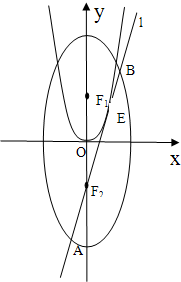 如圖,已知橢圓C:
如圖,已知橢圓C:| x2 |
| b2 |
| y2 |
| a2 |
| F2B |
| AF2 |
| ET |
| EF1 |
| EF2 |
| 1 |
| 2 |
| ET |
| OT |
| 5 |
| 4 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知橢圓C:
如圖,已知橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| F1A |
| F2A |
| π |
| 3 |
| 2π |
| 3 |
4
| ||
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如圖,已知橢圓C:
如圖,已知橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2012•梅州一模)如圖,已知橢圓C:
(2012•梅州一模)如圖,已知橢圓C:| x2 |
| a2 |
| AP |
| AQ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com