中文字幕人妻色偷偷久久-精品久久久久成人码免费动漫-久久精品国产清自在天天线-国产成人精品免高潮在线观看

精英家教網 > 高中數學 > 題目詳情

2×2矩陣M對應的變換將點(1,-1)與(-2,1)分別變換成點(-1,-1)與(0,-2).

(1)求矩陣M.

(2)設直線l在矩陣M對應的變換作用下得到了直線m:x-y=4.求直線l的方程.

 

(1) (2) x+y+2=0

【解析】(1)設M=,

則有=,

=,

所以且

解得所以M=.

(2)設直線l上一點為(x,y)在矩陣M對應的變換作用下變為(x',y'),

因為==且直線m:x'-y'=4,所以(x+2y)-(3x+4y)=4,

即x+y+2=0為直線l的方程.

 

練習冊系列答案
相關習題

科目：高中數學 來源：2014年高考數學全程總復習課時提升作業三十三第五章第四節練習卷（解析版） 題型：解答題

已知數列{an}的首項為a1=1,其前n項和為Sn,且對任意正整數n有n,an,Sn成等差數列.

(1)求證:數列{Sn+n+2}成等比數列.

(2)求數列{an}的通項公式.

 

查看答案和解析>>

科目：高中數學 來源：2014年高考數學全程總復習課時提升作業三十一第五章第二節練習卷（解析版） 題型：填空題

若Sn是等差數列{an}的前n項和,且S8-S3=10,則S11的值為　　　　.

 

查看答案和解析>>

科目：高中數學 來源：2014年高考數學全程總復習課時提升作業七十第十章第七節練習卷（解析版） 題型：選擇題

將一枚硬幣連擲5次,如果出現k次正面向上的概率等于出現k+1次正面向上的概率,那么k的值為(　　)

(A)0 (B)1 (C)2 (D)3

 

查看答案和解析>>

科目：高中數學 來源：2014年高考數學全程總復習課時提升作業七十四選修4-2第一節練習卷（解析版） 題型：解答題

在平面直角坐標系中,一種線性變換對應的2×2矩陣為.

(1)求點A(,3)在該變換作用下的象.

(2)求圓x2+y2=1在該變換作用下的新曲線的方程.

 

查看答案和解析>>

科目：高中數學 來源：2014年高考數學全程總復習課時提升作業七十六選修4-2第三節練習卷（解析版） 題型：解答題

對任意實數x,矩陣總存在特征向量,求m的取值范圍.

 

查看答案和解析>>

科目：高中數學 來源：2014年高考數學全程總復習課時提升作業七十八選修4-4第二節練習卷（解析版） 題型：解答題

在平面直角坐標系xOy中,曲線C1的參數方程為(φ為參數),曲線C2的參數方程為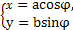(a>b>0,φ為參數),在以O為極點,x軸的正半軸為極軸的極坐標系中,射線l:θ=α與C1,C2各有一個交點.當α=0時,這兩個交點間的距離為2,當α=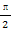時,這兩個交點重合.

(1)分別說明C1,C2是什么曲線,并求出a與b的值.

(2)設當α=時,l與C1,C2的交點分別為A1,B1,當α=-時,l與C1,C2的交點為A2,B2,求四邊形A1A2B2B1的面積.

 

查看答案和解析>>

科目：高中數學 來源：2014年高考數學全程總復習課時提升作業七十五選修4-2第二節練習卷（解析版） 題型：解答題

已知A=,B=,C=,求AB和AC.

 

查看答案和解析>>

科目：高中數學 來源：2014年高考數學全程總復習課時提升作業七十七選修4-4第一節練習卷（解析版） 題型：解答題

在極坐標系下,已知圓O:ρ=cosθ+sinθ和直線l:ρsin(θ-)=.

(1)求圓O和直線l的直角坐標方程.

(2)當θ∈(0,π)時,求直線l與圓O公共點的一個極坐標.

 

查看答案和解析>>

同步練習冊答案