
座落于我市紅梅公園邊的天寧寶塔堪稱中華之最,也堪稱佛塔世界之最.如圖,已知天寧寶塔AB高度為150米,某大樓CD高度為90米,從大樓CD頂部C看天寧寶塔AB的張角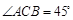 ,求天寧寶塔AB與大樓CD底部之間的距離BD.
,求天寧寶塔AB與大樓CD底部之間的距離BD.
180米.
解析試題分析:本題難點在于選擇函數解析式模型,是用余弦定理解三角形,還是取直角三角形表示邊.如用余弦定理解三角形,則得 ,解此方程成為難點;如構造直角三角形就會減少運算量,即作CE
,解此方程成為難點;如構造直角三角形就會減少運算量,即作CE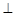 AB于E,構造直角三角形CBE和直角三角形CAE,利用兩角和的正切公式得到關于BD的方程
AB于E,構造直角三角形CBE和直角三角形CAE,利用兩角和的正切公式得到關于BD的方程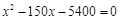 ,解此方程的運算量要少得多.將一個已知角分為兩個角的和,這種思維不常見,須多加注意,深刻體會.
,解此方程的運算量要少得多.將一個已知角分為兩個角的和,這種思維不常見,須多加注意,深刻體會.
試題解析:解:如圖作CE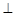 AB于E.因為AB∥CD,AB=150,CD=90,
AB于E.因為AB∥CD,AB=150,CD=90,
所以BE=90,AE=60.設CE=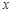 ,
, ,則
,則 . 2分
. 2分
在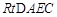 和
和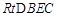 中,
中,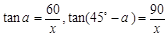 , 4分
, 4分
因為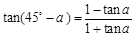 ,所以
,所以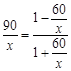 . 8分
. 8分
化簡得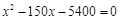 ,解得
,解得 或
或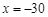 (舍去). 10分
(舍去). 10分
答:天寧寶塔AB與大樓CD底部之間的距離為180米. 12分
考點:兩角和的正切公式,函數與方程.


 名師指導期末沖刺卷系列答案
名師指導期末沖刺卷系列答案 開心蛙口算題卡系列答案
開心蛙口算題卡系列答案科目:高中數學 來源: 題型:解答題
如圖,在△ABC中,B=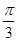 ,BC=2,點D在邊AB上,AD=DC,DE⊥AC,E為垂足.
,BC=2,點D在邊AB上,AD=DC,DE⊥AC,E為垂足.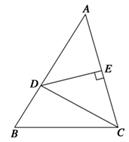
(1)若△BCD的面積為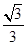 ,求CD的長;
,求CD的長;
(2)若ED=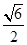 ,求角A的大小.
,求角A的大小.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com