
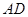 ⊥平面
⊥平面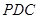 ,
,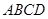 為平行四邊形,
為平行四邊形, 分別為
分別為 的中點,
的中點,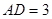 ,
,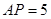 ,
,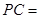
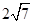 .
.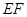 ∥平面
∥平面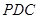 ;
;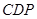 =90°,求證
=90°,求證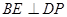 ;
;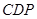 =120°,求該多面體的體積.
=120°,求該多面體的體積.
 。
。 ∥BC,且
∥BC,且 ,又ABCD為平行四邊形,
,又ABCD為平行四邊形, ∥BC,且
∥BC,且 ,
, ∥ED,且
∥ED,且
 平面PDC ∴EF∥平面PDC. ---------------------- 4分
平面PDC ∴EF∥平面PDC. ---------------------- 4分 平面ABCD,∴BE⊥DP ------------ 8分
平面ABCD,∴BE⊥DP ------------ 8分 與
與 面積相等,
面積相等, 與三棱錐
與三棱錐 體積相等,
體積相等, 體積的二倍.
體積的二倍. ,
, , 解得DC=2 ------------------- 10分
, 解得DC=2 ------------------- 10分 三棱錐
三棱錐 的體積
的體積
 -------------------- 12分
-------------------- 12分

科目:高中數學 來源:不詳 題型:單選題
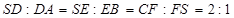 ,若仍用該容器盛水,最多盛水(可以任意情形放置)為原三棱錐體積的( )
,若仍用該容器盛水,最多盛水(可以任意情形放置)為原三棱錐體積的( )
A. | B.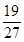 | C.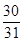 | D.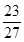 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:單選題
A.1∶ | B.1∶9 | C.1∶ | D.1∶ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com